
【题目】为了“迎国庆,向祖国母亲献礼”,某建筑公司承建了修筑一段公路的任务,指派甲、乙两队合作,18天可以完成,共需施工费126000元;如果甲、乙两队单独完成此项工程,乙队所用时间是甲队的1.5倍,乙队每天的施工费比甲队每天的施工费少1000元.
(1)甲、乙两队单独完成此项工程,各需多少天?
(2)为了尽快完成这项工程任务,甲、乙两队通过技术革新提高了速度,同时,甲队每天的施工费提高了![]() ,乙队每天的施工费提高了
,乙队每天的施工费提高了![]() ,已知两队合作12天后,由甲队再单独做2天就完成了这项工程任务,且所需施工费比计划少了21200元.
,已知两队合作12天后,由甲队再单独做2天就完成了这项工程任务,且所需施工费比计划少了21200元.
①分别求出甲、乙两队技术革新前每天的施工费用;
②求![]() 的值.
的值.
【答案】(1)甲公司单独完成此项工程需30天,乙公司单独完成此项工程需45天;(2)①技术革新前,甲公司每天的施工费用是4000元,乙公司每天的施工费用是3000元;②a=10.
【解析】
(1)设甲公司单独完成此项工程需x天,直接利用甲、乙两公司合做,18天可以完成,利用两公司合作每天完成总量的![]() ,进而列出方程求出答案;
,进而列出方程求出答案;
(2)①设甲公司技术革新前每天的施工费用是y元,那么乙公司技术革新前每天的施工费用是(y-1000)元,可列方程(y+y-1000)×18=126000,解方程即可;
②根据①可分别表示甲、乙公司技术革后每天的施工费用,于是可列方程,解方程即可.
解:(1)设甲公司单独完成此项工程需x天,根据题意可得:
![]() ,
,
解得:x=30,
检验,知x=30符合题意,
∴1.5x=45,
答:甲公司单独完成此项工程需30天,乙公司单独完成此项工程需45天;
(2)①设甲公司技术革新前每天的施工费用是y元,那么乙公司技术革新前每天的施工费用是(y-1000)元,
则由题意可得:(y+y-1000)×18=126000,
解得:y=4000,
∴y-1000=3000,
答:技术革新前,甲公司每天的施工费用是4000元,乙公司每天的施工费用是3000元;
②4000×14×(1+a%)+3000×12×(1+2a%)=126000-21200,
解得:a=10.
答:![]() 的值是10.
的值是10.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,对角线AC与BD相交于点O,点E是BC上的一个动点,连接DE, 交 AC于点F.
(1)如图①,当![]() 时,求
时,求![]() 的值;
的值;
(2)如图②当DE平分∠CDB时,求证:AF=![]() OA;
OA;
(3)如图③,当点E是BC的中点时,过点F作FG⊥BC于点G,求证:CG=![]() BG.
BG.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知菱形ABCD的对角线AC、BD相交于点O,延长AB至点E,使BE=AB,连接CE.

(1)求证:四边形BECD是平行四边形;
(2)若∠E=60°,AC=![]() ,求菱形ABCD的面积.
,求菱形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AF∥CD,CB平分∠ACD,BD平分∠EBF,且BC⊥BD,下列结论:① BC平分∠ABE;② AC∥BE;③ ∠CBE+∠D=90°;④ ∠DEB=2∠ABC.其中正确结论的个数有( )

A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
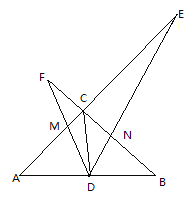
【题目】如图,在△ABC中,∠ACB=90°,CD是中线,AC=BC,一个以点D为顶点的45°角绕点D旋转,使角的两边分别与AC、BC的延长线相交,交点分别为E、F,DF与AC交于点M,DE与BC交于点N。
(1)求证:△ADM∽△BND;
(2)在∠EDF绕点D旋转的过程中:
①探究三条线段CD、CE、CF之间的数量关系,并说明理由;
②若CE=4,CF=2,求DN的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△ABC的顶点坐标分别为A(﹣3,2),B(﹣4,1),C(﹣2,0).

(1)若将△ABC向右平移3个单位长度,再向上平移1个单位长度,请画出平移后的△A1B1C1;
(2)若△A2B2C2与△ABC是中心对称图形,则对称中心的坐标为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知反比例函数![]() 的图象的一支位于第一象限.
的图象的一支位于第一象限.
(1)判断该函数图象的另一支所在的象限,并求m的取值范围;
(2)如图,O为坐标原点,点A在该反比例函数位于第一象限的图象上,点B与点A关于![]() 轴对称,若△OAB的面积为6,求m的值.
轴对称,若△OAB的面积为6,求m的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
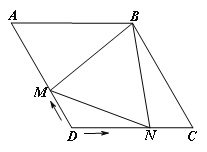
【题目】如图,菱形ABCD,∠A=60°,AB=6,点M从点D向点A以1个单位∕秒的速度运动,同时点N从点D向点C以2个单位∕秒的速度运动,连结BM、BN,当△BMN为等边三角形时,![]() =_____.
=_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com