
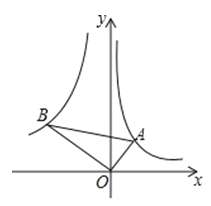
【题目】如图,点![]() 分别在反比例函数
分别在反比例函数![]() 的图象上.若
的图象上.若![]() ,
,![]() ,则的值为( )
,则的值为( )
A.![]() B.
B.![]() C.4D.2
C.4D.2
【答案】B
【解析】
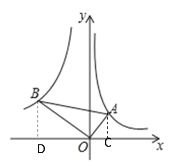
分别过点A作AC⊥x轴于C,过点B作BD⊥x轴于D,根据点A所在的图象可设点A的坐标为(x, ![]() ),根据相似三角形的判定证出△BDO∽△OCA,列出比例式即可求出点B的坐标,然后代入
),根据相似三角形的判定证出△BDO∽△OCA,列出比例式即可求出点B的坐标,然后代入![]() 中即可求出a的值.
中即可求出a的值.
解:分别过点A作AC⊥x轴于C,过点B作BD⊥x轴于D,
∵点A在反比例函数![]() 上,
上,
设点A的坐标为(x, ![]() ),则OC=x,AC=
),则OC=x,AC=![]() ,
,
∴∠BDO=∠OCA=90°
∵OA⊥OB,
∴∠BOD+∠AOC=180°-∠AOB=90°,∠OAC+∠AOC=90°
∴∠BOD=∠OAC
∴△BDO∽△OCA
∴![]()
解得:OD=2AC=![]() ,BD=2OC=2x,
,BD=2OC=2x,
∵点B在第二象限
∴点B的坐标为(![]() ,2x)
,2x)
将点B坐标代入![]() 中,解得a=﹣4
中,解得a=﹣4
故选B.


 发散思维新课堂系列答案
发散思维新课堂系列答案科目:初中数学 来源: 题型:
【题目】小明和小李准备七月初到重庆或长沙去旅游,为了了解这两个城市哪个更热,他们查阅资料,收集了两个城市2018年七月前两周最高温度的记录,如下表
日期(七月) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
重庆最高温度/℃ | 33 | 36 | 34 | 31 | 31 | 30 | 30 | 33 | 34 | 36 | 37 | 35 | 37 | 37 |
长沙最高温度/℃ | 29 | 34 | 35 | 35 | 36 | 29 | 31 | 31 | 34 | 35 | 35 | 31 | 35 | 35 |
根据上表,他们将两个城市的最高温度分别绘制了如下的频数分布直方图和统计表,并对数据进行了整理
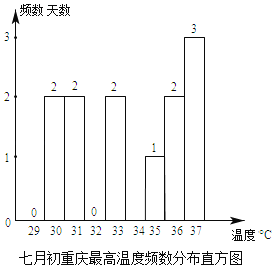
最高温度/℃ | 天数 | ||||||
28≤x<30 | 2 | ||||||
30≤x<32 | a | ||||||
32≤x<34 | 0 | ||||||
34≤x<36 | 8 | ||||||
36≤x<38 | 1 | ||||||
平均数/℃ | 中位数/℃ | 众数/℃ | 34℃以上天数 | 30℃以下天数 | |||
重庆 | 33.9 | 34 | c | 6 | 0 | ||
长沙 | 33.2 | b | 35 | 7 | 2 | ||
回答如下问题
(1)本次调查的目的是 ;
(2)补全频数分布直方图并写出表中a,b,c的值,a= ,b= ,c= ;
(3)结合以上分析,你认为七月初哪个城市更热,请写出两条支持你观点的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
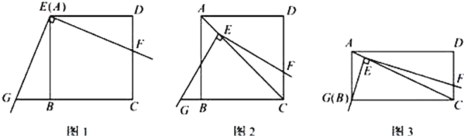
【题目】如图1,将三角板放在正方形![]() 上,使三角板的直角顶点
上,使三角板的直角顶点![]() 与正方形
与正方形![]() 的顶点
的顶点![]() 重合,三角板的一边交
重合,三角板的一边交![]() 于点
于点![]() .另一边交
.另一边交![]() 的延长线于点
的延长线于点![]() .
.
(1)观察猜想:线段![]() 与线段
与线段![]() 的数量关系是_____;
的数量关系是_____;
(2)探究证明:如图2,移动三角板,使顶点![]() 始终在正方形
始终在正方形![]() 的对角线
的对角线![]() 上,其他条件不变,(1)中的结论是否仍然成立?若成立,请给予证明:若不成立.请说明理由:
上,其他条件不变,(1)中的结论是否仍然成立?若成立,请给予证明:若不成立.请说明理由:
(3)拓展延伸:如图3,将(2)中的“正方形![]() ”改为“矩形
”改为“矩形![]() ”,且使三角板的一边经过点
”,且使三角板的一边经过点![]() ,其他条件不变,若
,其他条件不变,若![]() 、
、![]() ,请探究线段
,请探究线段![]() 与线段
与线段![]() 之间存在怎样的数量关系?(用含
之间存在怎样的数量关系?(用含![]() 、
、![]() 的代数式表示)
的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知等边△ABC,以AB为直径的圆与BC边交于点D,过点D作DF⊥AC,垂足为F.
(1)求证:DF是⊙O的切线;
(2)过点F作FG⊥AB,垂足为G,若AB=12.
①求FG的长;
②求点D到FG的距离.

查看答案和解析>>
科目:初中数学 来源: 题型:
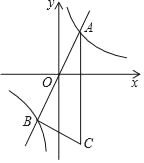
【题目】如图,反比例函数的图象与正比例函数y=2x的图象相交于A(1,a),B两点,点C在第四象限,CA∥y轴,∠ABC=90°
(1)求反比例函数的解析式及点B的坐标;
(2)求tanC的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂生产部门为了解本部门工人的生产能力情况,进行了抽样调查.该部门随机抽取了30名工人某天每人加工零件的个数,数据如下:
20 | 21 | 19 | 16 | 27 | 18 | 31 | 29 | 21 | 22 |
25 | 20 | 19 | 22 | 35 | 33 | 19 | 17 | 18 | 29 |
18 | 35 | 22 | 15 | 18 | 18 | 31 | 31 | 19 | 22 |
整理上面数据,得到条形统计图:
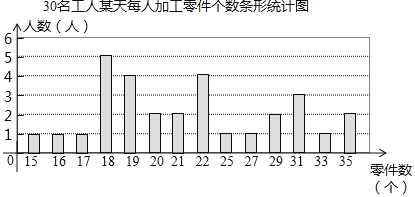
样本数据的平均数、众数、中位数如下表所示:
统计量 | 平均数 | 众数 | 中位数 |
数值 | 23 | m | 21 |
根据以上信息,解答下列问题:
(1)上表中众数m的值为 ;
(2)为调动工人的积极性,该部门根据工人每天加工零件的个数制定了奖励标准,凡达到或超过这个标准的工人将获得奖励.如果想让一半左右的工人能获奖,应根据 来确定奖励标准比较合适.(填“平均数”、“众数”或“中位数”)
(3)该部门规定:每天加工零件的个数达到或超过25个的工人为生产能手.若该部门有300名工人,试估计该部门生产能手的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
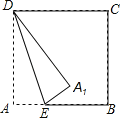
【题目】如图,已知正方形ABCD,边长为8,E是AB边上的一点,连接DE,将△DAE沿DE所在直线折叠,使点A的对应点A1落在正方形的边CD或BC的垂直平分线上,则AE的长度是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 的图象与抛物线
的图象与抛物线![]() 交
交![]() 轴于
轴于![]() 点,交
点,交![]() 轴于
轴于![]() 点,抛物线交
点,抛物线交![]() 轴的另一个交点为点
轴的另一个交点为点![]() (点
(点![]() 的左边).点
的左边).点![]() 为抛物线上一个动点(且点
为抛物线上一个动点(且点![]() 的横坐标
的横坐标![]() 满足
满足![]() ,过点
,过点![]() 作
作![]() 轴交
轴交![]() 于点
于点![]() .
.
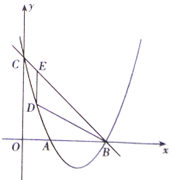
(1)求该抛物线的解析式;
(2)若![]() 为直角三角形,求点
为直角三角形,求点![]() 的坐标;
的坐标;
(3)在(2)的结论下,点![]() 为抛物线上任意一个动点,点
为抛物线上任意一个动点,点![]() 为
为![]() 轴上一个动点,则以
轴上一个动点,则以![]() ,
,![]() ,
,![]() ,
,![]() 四点为顶点的四边形能否为平行四边形,若能,请直接写出点
四点为顶点的四边形能否为平行四边形,若能,请直接写出点![]() 的坐标;若不能,请说明理由.
的坐标;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】疫情期间,甲厂欲购买某种无纺布生产口罩,A、B两家无纺布公司各自给出了该种无纺布的销售方案.
A公司方案:无纺布的价格均为每吨1.95万元![]() ;
;
B公司方案:无纺布不超过30吨时,每吨收费2万元;超过30吨时,超过的部分每吨收费1.9万元.
设甲厂在同一公司一次购买无纺布的数量为x吨(x>0).
(Ⅰ)根据题意,填写下表:
一次购买数量(吨) | 10 | 20 | 35 | … |
A公司花费(万元) | 39 | … | ||
B公司花费(万元) | 40 | … |
(Ⅱ) 设在A公司花费![]() 万元,在B公司花费
万元,在B公司花费![]() 万元,分别求
万元,分别求![]() 、
、![]() 关于x的函数解析式;
关于x的函数解析式;
(Ⅲ)如果甲厂所需购买的无纺布是50吨,试通过计算说明选择哪家公司费用较少.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com