练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    1．为整治城市街道的汽车超速现象，交警大队在某街道旁进行了流动测速．如图，一辆小汽车在某城市街道上直行，某一时刻刚好行驶到离车速检测仪A60m的C处，过了4s后，小汽车到达离车速检测仪A100m的B处，已知该段城市街道的限速为60km/h，请问这辆小汽车是否超速？

    分析 直接利用勾股定理得出BC的长，进而得出汽车的速度，即可比较得出答案．

    解答 解：超速．理由如下：
    在Rt△ABC中，AC=60m，AB=100m，
    由勾股定理可得BC=$\sqrt{A{B}^{2}-A{C}^{2}}$=$\sqrt{10{0}^{2}-6{0}^{2}}$=80m，
    ∴汽车速度为80÷4=20m/s=72km/h，
    ∵72＞60，
    ∴这辆小汽车超速了．

    点评 此题主要考查了勾股定理的应用，根据题意得出汽车的速度是解题关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    9．计算
    （1）（-$\frac{1}{4}$）-2-（-2016）0+（$\frac{2}{3}$）11•（-1$\frac{1}{2}$）12
    （2）（3x-2）2+（-3+x）（-x-3）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

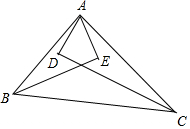    12．如图，已知BE，CD是△ABC的角平分线，并且AE⊥BE于点E，AD⊥DC于点D，求证：
    （1）DE∥BC
    （2）DE=$\frac{1}{2}$（AB+AC-BC）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    9．如图，在平面直角坐标系中，点A在X轴正半轴上，B在Y轴的负半轴，过点B画MN∥x轴；C是Y轴上一点，连接AC，作CD⊥CA．
    （1）如图（1），请直接写出∠CA0与∠CDB的数量关系．
    （2）如图（2），在题（1）的条件下，∠CAO的角平分线与∠CDB的角平分线相交于点P，求∠APD的度数．
    （3）如图（2），在题（1）、（2）的条件下，∠CAX的角平分线与∠CDN的角平分线相交于点Q，请直接写出∠APD与∠AQD数量关系．
    （4）如图（3），点C在Y轴的正半轴上运动时，∠CAO的角平分线所在的直线与∠CDB的角平分线相交于点P，∠APD的大小是否变化？若不变，直接写出其值；若变化，说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

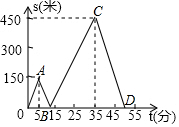    16．甲、乙两人匀速从同一地点到1500米处的图书馆看书，甲出发5分钟后，乙以50米/分的速度沿同一路线行走，设甲、乙两人相距s（米），甲行走的时间为t（分），s关于t的函数图象如图所示．
    （1）求乙出发多长时间后能追上甲？
    （2）求直线BC的函数表达式；
    （3）当甲、乙两人相距330米时，求t的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    6．先阅读，再回答问题：要比较代数式A、B的大小，可以作差A-B，比较差的取值，当A-B＞0时，有A＞B；当A-B=0时，有A=B；当A-B＜0时，有A＜B．”例如，当a＜0时，比较a2和a（a+1）的大小．可以观察a2-a（a+1）=a2-a2-a=-a．因为当a＜0时，-a＞0，所以当a＜0时，a2＞a（a+1）．
    （1）已知M=（x-2）（x-16），N=（x-4）（x-8），比较M、N的大小关系．
    （2）某种产品的原料提价，因而厂家决定对于产品进行提价，现有三种方案：
    方案1：第一次提价p%，第二次提价q%；
    方案2：第一次提价q%，第二次提价p%；
    方案3：第一、二次提价均为$\frac{p+q}{2}$%．
    如果设原价为a元，请用含a、p、q的式子表示提价后三种方案的价格．
    方案1：a（1+p%）（1+q%）；方案2：a（1+p%）（1+q%）；方案3：a（1+$\frac{p+q}{2}$%）2
    ?如果p，q是不相等的正数，三种方案哪种提价最多？

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    13．支付宝与“滴滴打车”联合推出优惠，“滴滴打车”一夜之间红遍大江南北，据统计，2016年“滴滴打车”账户流水总金额达到4730000000元，用科学记数法表示为（　　）
    A．4.73×108B．4.73×109C．4.73×1010D．4.73×1011

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

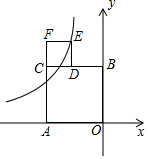    10．如图，四边形AOBC和四边形CDEF都是正方形，边OA在x轴上，边OB在y轴上，点D在边CB上，反比例函数y=$-\frac{8}{x}$在第二象限的图象经过点E，则正方形AOBC和正方形CDEF的面积之差为（　　）
    A．12B．10C．8D．6

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    11．正方形ABCD中，M，N分别是CB，DC延长线上的一点，且有DN-BM=MN．
    （1）求证：∠MAN=45°．
    （2）过点D作DP⊥AN交AM于P，连CP，求线段PA，PC，PD之间的数量关系．
    （3）若点C为DN的中点，且AB=1，求CP的长．

    查看答案和解析>>

    同步练习册答案