
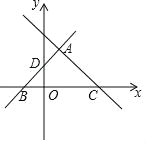
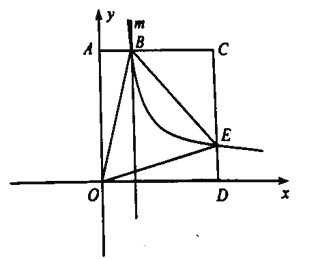
【题目】如图,在平面直角坐标系中,直线y=﹣x+3与x轴交于点C与直线AD交于点A(1,2),点D的坐标为(0,1)
(1)求直线AD的解析式;
(2)直线AD与x轴交于点B,请判断△ABC的形状;
(3)在直线AD上是否存在一点E,使得4S△BOD=S△ACE,若存在求出点E的坐标,若不存在说明理由.
【答案】(1)y=x+1;(2)△ABC是等腰直角三角形;(3)存在,点E的坐标为(2,3)或(0,1)时,4S△BOD=S△ACE.
【解析】
(1)利用待定系数法,即可得到直线AD的解析式;
(2)依据点的坐标求得AB=2![]() ,AC=2
,AC=2![]() ,BC=4,即可得到AB2+AC2=16=BC2,进而得出△ABC是等腰直角三角形;
,BC=4,即可得到AB2+AC2=16=BC2,进而得出△ABC是等腰直角三角形;
(3)依据4S△BOD=S△ACE,即可得到AE=![]() ,分两种情况进行讨论:①点E在直线AC的右侧,②点E在直线AC的左侧,分别依据AD=AE=
,分两种情况进行讨论:①点E在直线AC的右侧,②点E在直线AC的左侧,分别依据AD=AE=![]() ,即可得到点E的坐标.
,即可得到点E的坐标.
解:(1)直线AD的解析式为y=kx+b,
∵直线AD经过点A(1,2),点D(0,1),
∴![]() ,
,
解得![]() ,
,
∴直线AD的解析式为y=x+1;
(2)∵y=x+1中,当y=0时,x=﹣1;y=﹣x+3中,当y=0时,x=3,
∴直线AD与x轴交于B(﹣1,0),直线AC与x轴交于C(3,0),
∵点A(1,2),
∴AB=2![]() ,AC=2
,AC=2![]() ,BC=4,
,BC=4,
∵AB2+AC2=16=BC2,
∴∠BAC=90°,
∴△ABC是等腰直角三角形;
(3)存在,
AC=2![]() ,S△BOD=
,S△BOD=![]() ×1×1=
×1×1=![]() ,
,
∵△ABC是等腰直角三角形,
∴∠CAE=90°,
∵S△ACE=![]() AE×AC,4S△BOD=S△ACE,
AE×AC,4S△BOD=S△ACE,
∴4×![]() =
=![]() ×AE×2
×AE×2![]() ,
,
解得AE=![]() ,
,
①如图,当点E在直线AC的右侧时,过E作EF⊥y轴于F,
∵AD=AE=![]() ,∠EDF=45°,
,∠EDF=45°,
∴EF=DF=2,OF=2+1=3,
∴E(2,3);
②当点E在直线AC的左侧时,
∵AD=AE=![]() ,
,
∴点E与点D重合,即E(0,1),
综上所述,当点E的坐标为(2,3)或(0,1)时,4S△BOD=S△ACE.



科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象的顶点在第一象限,且过点(0,1)和(﹣1,0),下列结论:①ab<0,②b2>4,③0<a+b+c<2,④0<b<1,⑤当x>﹣1时,y>0.其中正确结论的个数是( )

A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
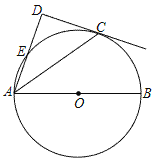
【题目】如图,点C在以AB为直径的⊙O上,AD与过点C的切线垂直,垂足为点D,AD交⊙O于点E.
(1) 求证:AC平分∠DAB;
(2) 连接BE交AC于点F,若cos∠CAD=![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图![]() ,
,![]() 分别为数轴上的两点,
分别为数轴上的两点,![]() 点对应的数为-10,
点对应的数为-10,![]() 点对应的数为90.
点对应的数为90.

(1)![]() ,
,![]() 两点间的距离为________.
两点间的距离为________.
(2)现在有一只电子蚂蚁![]() 从
从![]() 点出发,以2个单位/秒的速度向右运动,同时另一只电子蚂蚁
点出发,以2个单位/秒的速度向右运动,同时另一只电子蚂蚁![]() 恰好从
恰好从![]() 点出发,以3个单位/秒的速度向左运动.运动时间为
点出发,以3个单位/秒的速度向左运动.运动时间为![]() 秒,用含
秒,用含![]() 的代数式表示:
的代数式表示:
①点![]() 在数轴上表示的数为________.
在数轴上表示的数为________.
②若两只电子蚂蚁在数轴上的![]() 点相遇,则
点相遇,则![]() 点对应的数是多少.
点对应的数是多少.
(3)若当电子蚂蚁![]() 从
从![]() 点出发时,以4个单位/秒的速度向左运动,同时另一只电子蚂蚁
点出发时,以4个单位/秒的速度向左运动,同时另一只电子蚂蚁![]() 恰好从
恰好从![]() 点出发,以6个单位/秒的速度向左运动,经过多长的时间两只电子蚂蚁在数轴上相距20个单位长度.
点出发,以6个单位/秒的速度向左运动,经过多长的时间两只电子蚂蚁在数轴上相距20个单位长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为弘扬中华优秀传统文化,某校开展“经典诵读”比赛活动,诵读材料有《论语》、《大学》、《中庸》(依次用字母A,B,C表示这三个材料),将A,B,C分别写在3张完全相同的不透明卡片的正面上,背面朝上洗匀后放在桌面上,比赛时小礼先从中随机抽取一张卡片,记下内容后放回,洗匀后,再由小智从中随机抽取一张卡片,他俩按各自抽取的内容进行诵读比赛.
(1)小礼诵读《论语》的概率是 ;(直接写出答案)
(2)请用列表或画树状图的方法求他俩诵读两个不同材料的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
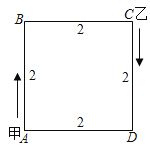
【题目】正方形ABCD的轨道上有两个点甲与乙,开始时甲在A处,乙在C处,它们沿着正方形轨道顺时针同时出发,甲的速度为每秒1cm,乙的速度为每秒5cm,已知正方形轨道ABCD的边长为2cm,则乙在第2019次追上甲时的位置在( )
A.AB上B.BC上C.CD上D.AD上
查看答案和解析>>
科目:初中数学 来源: 题型:
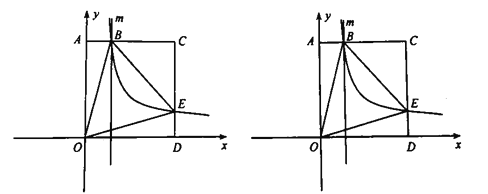
【题目】如图,边长为3正方形![]() 的顶点
的顶点![]() 与原点重合,点
与原点重合,点![]() 在
在![]() 轴,
轴,![]() 轴上。反比例函数
轴上。反比例函数![]() 的图象交
的图象交![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() .
.
(1)求反比例函数的解析式;
(2)过点![]() 作
作![]() 轴的平行线
轴的平行线![]() ,点
,点![]() 在直线
在直线![]() 上运动,点
上运动,点![]() 在
在![]() 轴上运动.
轴上运动.
①若![]() 是以
是以![]() 为直角顶点的等腰直角三角形,求
为直角顶点的等腰直角三角形,求![]() 的面积;
的面积;
②将“①”中的“以![]() 为直角顶点的”去掉,将问题改为“若
为直角顶点的”去掉,将问题改为“若![]() 是等腰直角三角形”,
是等腰直角三角形”,![]() 的面积除了“①”中求得的结果外,还可以是______.(直接写答案,不用写步骤)
的面积除了“①”中求得的结果外,还可以是______.(直接写答案,不用写步骤)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com