
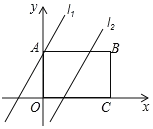
ЁОЬтФПЁПШчЭМЃЌдкОиаЮABCDжаЃЌЕуOЮЊзјБъдЕуЃЌЕуBЕФзјБъЮЊ(4ЃЌ3)ЃЌЕуAЁЂCдкзјБъжсЩЯЃЌЕуPдкBCБпЩЯЃЌжБЯп11ЃКy=2x+3ЃЌжБЯп12ЃКy=2xЉ3ЃЎ
ЃЈ1ЃЉЗжБ№ЧѓжБЯп11гыxжсЁЂжБЯп12гыABЕФНЛЕуDКЭEЕФзјБъЃЛ
ЃЈ2ЃЉвбжЊЕуMдкОиаЮABCDФкВПЃЌЧвЪЧжБЯп12ЩЯЕФЕуЃЌШєЁїAPMЪЧЕШбќжБНЧШ§НЧаЮЃЌЧѓЕуMЕФзјБъЃЛ
ЃЈ3ЃЉЮвУЧАбжБЯп11КЭжБЯп12ЩЯЕФЕуЫљзщГЩЕФЭМаЮГЦЮЊЭМаЮFЃЎвбжЊОиаЮANPQЕФЖЅЕуNдкЭМаЮFЩЯЃЌЧвдкAPЕФЩЯЗНЃЌQЪЧзјБъЦНУцФкЕФЕуЃЌЩшNЕуЕФКсзјБъЮЊxЃЌЧыжБНгаДГіxЕФШЁжЕЗЖЮЇ(ВЛБиЫЕУїРэгЩ)ЃЎ
ЁОД№АИЁПЃЈ1ЃЉ(![]() ЃЌ0)ЃЌ(3ЃЌ3)ЃЛЃЈ2ЃЉЕуMЕФзјБъЮЊ(2ЃЌ1)ЃЛЃЈ3ЃЉ0ЃМx
ЃЌ0)ЃЌ(3ЃЌ3)ЃЛЃЈ2ЃЉЕуMЕФзјБъЮЊ(2ЃЌ1)ЃЛЃЈ3ЃЉ0ЃМx![]() Лђ
Лђ![]() x
x![]() ЃЎ
ЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнзјБъжсЩЯЕуЕФзјБъЬиеїПЩЧѓжБЯпl1гыxжсЃЌжБЯпl2гыABЕФНЛЕузјБъЃЛ
ЃЈ2ЃЉЗжШ§жжЧщПіЃКЂйШєЕуAЮЊжБНЧЖЅЕуЪБЃЌЕуMдкЕквЛЯѓЯоЃЛЂкШєЕуPЮЊжБНЧЖЅЕуЪБЃЌЕуMдкЕквЛЯѓЯоЃЛЂлШєЕуMЮЊжБНЧЖЅЕуЪБЃЌЕуMдкЕквЛЯѓЯоЃЛНјааЬжТлЃЌдйПДЕуMЪЧЗёдкОиаЮABCDФкВПЃЌМДПЩЧѓЕуMЕФзјБъЃЛ
ЃЈ3ЃЉИљОнОиаЮЕФаджЪКЭNдкAPЕФЩЯЗНЃЌПЩЧѓNЕуЕФКсзјБъxЕФШЁжЕЗЖЮЇЃЎ
ЃЈ1ЃЉжБЯпl1ЃКЕБy=0ЪБЃЌ2x+3=0ЃЌx![]() ЃЌ
ЃЌ
дђжБЯпl1гыxжсзјБъЮЊ(![]() ЃЌ0)
ЃЌ0)
жБЯпl2ЃКЕБy=3ЪБЃЌ2xЉ3=3ЃЌx=3
дђжБЯпl2гыABЕФНЛЕузјБъЮЊ(3ЃЌ3)ЃЛ
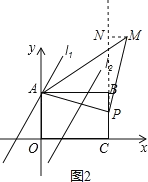
ЃЈ2ЃЉЂйШєЕуAЮЊжБНЧЖЅЕуЪБЃЌЕуMдкЕквЛЯѓЯоЃЌСЌНсACЃЌШчЭМ1ЫљЪОЃК
ЁЯAPBЃОЁЯACBЃО45ЁуЃЌЁрЁїAPMВЛПЩФмЪЧЕШбќжБНЧШ§НЧаЮЃЌЁрЕуMВЛДцдкЃЛ
ЂкШєЕуPЮЊжБНЧЖЅЕуЪБЃЌЕуMдкЕквЛЯѓЯоЃЌШчЭМ2ЫљЪОЃК
Й§ЕуMзїMNЁЭCBЃЌНЛCBЕФбгГЄЯпгкЕуNЃЌ
дђЁЯPNM=ЁЯABP=90ЁуЃЌЁЯBAP=ЁЯNPMЃЌ
дкЁїABPКЭЁїPNMжаЃЌ ЃЌЁрЁїABPЁеЁїPNM(AAS)ЃЌЁрAB=PN=4ЃЌMN=BPЃЌ
ЃЌЁрЁїABPЁеЁїPNM(AAS)ЃЌЁрAB=PN=4ЃЌMN=BPЃЌ
ЩшM(xЃЌ2xЉ3)ЃЌдђMN=xЉ4ЃЌЁр2xЉ3=4+3Љ(xЉ4)ЃЌ
x![]() ЃЌЁрM(
ЃЌЁрM(![]() ЃЌ
ЃЌ![]() )ЃЌ
)ЃЌ
ЕуMдкЕквЛЯѓЯоЃЌЕЋВЛдкОиаЮABCDФкВПЃЌВЛКЯЬтвтЩсШЅЃЛ
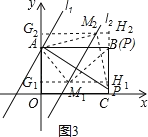
ЂлШєЕуMЮЊжБНЧЖЅЕуЪБЃЌЕуMдкЕквЛЯѓЯоЃЌШчЭМ3ЫљЪОЃК
ЩшM1(xЃЌ2xЉ3)ЃЌ
Й§ЕуM1зїM1G1ЁЭOAЃЌНЛBCгкЕуH1ЃЌ
ЭЌРэЃКЁїAM1G1ЁеЁїPM1H1(AAS)ЃЌ
ЁрAG1=M1H1=3Љ(2xЉ3)ЃЌ
Ёрx+3Љ(2xЉ3)=4ЃЌ
x=2ЃЌЁрM1(2ЃЌ1)ЃЛ
ЩшM2(xЃЌ2xЉ3)ЃЌ
ЭЌРэПЩЕУx+2xЉ3Љ3=4ЃЌЁрx![]() ЃЌ
ЃЌ
ЁрM2(![]() ЃЌ
ЃЌ![]() )ЃЌ
)ЃЌ
ЕуM2дкЕквЛЯѓЯоЃЌЕЋВЛдкОиаЮABCDФкВПЃЌВЛКЯЬтвтЩсШЅЃЛ
ЁрЕуMЕФзјБъЮЊ(2ЃЌ1)ЃЛ
ЃЈ3ЃЉЕБЕуNдкжБЯпl2ЩЯЪБЃЎ
ЁпЕуNЕФКсзјБъЮЊxЃЌ
ЁрN(xЃЌ2xЉ3)ЃЌ
ЕБЕуPКЭЕуBжиКЯЪБЃЌP(4ЃЌ3)ЃЌ
Й§NзїNHЁЭABгкHЃЌдђЁїNHGЪЧжБНЧШ§НЧаЮЃЌШчЭМ4ЫљЪОЃК
ЁрAPЕФжаЕуGзјБъЮЊ(2ЃЌ3)ЃЎ
ЁпЫФБпаЮANPQЪЧОиаЮЃЌ
ЁрЁЯANB=90ЁуЃЌ
ЁрNG![]() AP=2ЃЌ
AP=2ЃЌ
Ёр(xЉ2)2+(2xЉ3Љ3)2=4ЃЌ
Ёрx![]() (ЕуNдкABЩЯЗНЕФКсзјБъ)Лђx=2(ЕуNдкAPЯТЗНЕФКсзјБъЃЌВЛКЯЬтвтЩсШЅ)ЃЌ
(ЕуNдкABЩЯЗНЕФКсзјБъ)Лђx=2(ЕуNдкAPЯТЗНЕФКсзјБъЃЌВЛКЯЬтвтЩсШЅ)ЃЌ
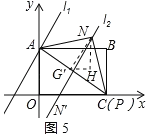
ЕБЕуPКЭЕуCжиКЯЪБЃЌСЌНгNG'ЃЌЙ§NзїNHЁЭG'HгкHЃЌ
дђЁїNHG'ЪЧжБНЧШ§НЧаЮЃЌШчЭМ5ЫљЪОЃК
P(4ЃЌ0)ЃЌAPЕФжаЕуG'зјБъЮЊ(2ЃЌ![]() )ЃЌ
)ЃЌ
ЭЌРэЃКNG'![]() AP
AP![]() ЃЌ
ЃЌ
Ёр(xЉ2)2+(2xЉ3![]() )2
)2![]() ЃЌ
ЃЌ
Ёрx![]() (ЕуNдкABЩЯЗНЙЙГЩЕФЫФБпаЮЪЧОиаЮЕФКсзјБъ)Лђx
(ЕуNдкABЩЯЗНЙЙГЩЕФЫФБпаЮЪЧОиаЮЕФКсзјБъ)Лђx![]() (ЕуNдкAPЯТЗНЙЙГЩЕФЫФБпаЮЪЧОиаЮЕФКсзјБъЃЌВЛКЯЬтвтЩсШЅ)ЃЌ
(ЕуNдкAPЯТЗНЙЙГЩЕФЫФБпаЮЪЧОиаЮЕФКсзјБъЃЌВЛКЯЬтвтЩсШЅ)ЃЌ
Ёр![]() x
x![]() ЃЌ
ЃЌ
ЕБЕуNдкl1ЩЯЪБЃЌ
ЕуPКЭЕуBжиКЯЪБЃЌСЌНгNGЃЌЙ§NзїNHЁЭABгкHЃЌ
дђЁїNHGЪЧжБНЧШ§НЧаЮЃЌШчЭМ6ЫљЪОЃК
ЭЌРэЃК(2Љx)2+x2=4ЃЌ
НтЕУЃКx![]() ЃЌЁр0ЃМx
ЃЌЁр0ЃМx![]() ЃЌ
ЃЌ
ЕБЕуPКЭЕуCжиКЯЪБЃЌNдкAPЕФЯТЗНЃЌВЛКЯЬтвтЃЌЁрxЕФШЁжЕЗЖЮЇЮЊЃК0ЃМx![]() Лђ
Лђ![]() x
x![]() ЃЎ
ЃЎ






| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌжБЯпy=2xгыЗДБШР§КЏЪ§y=![]() ЃЈxЃО0ЃЉЕФЭМЯѓНЛгкЕуAЃЈ4ЃЌnЃЉЃЌABЁЭxжсЃЌДЙзуЮЊBЃЎ
ЃЈxЃО0ЃЉЕФЭМЯѓНЛгкЕуAЃЈ4ЃЌnЃЉЃЌABЁЭxжсЃЌДЙзуЮЊBЃЎ
ЃЈ1ЃЉЧѓkЕФжЕЃЛ
ЃЈ2ЃЉЕуCдкABЩЯЃЌШєOC=ACЃЌЧѓACЕФГЄЃЛ
ЃЈ3ЃЉЕуDЮЊxжсе§АыжсЩЯвЛЕуЃЌдкЃЈ2ЃЉЕФЬѕМўЯТЃЌШєSЁїOCD=SЁїACDЃЌЧѓЕуDЕФзјБъЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
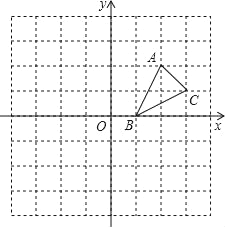
ЁОЬтФПЁПШчЭМЃЌЗНИёжНжаЕФУПИіаЁЗНИёЖМЪЧБпГЄЮЊ1ИіЕЅЮЛЕФе§ЗНаЮЃЌдкНЈСЂЦНУцжБНЧзјБъЯЕКѓЃЌЁїABCЕФЖЅЕуОљдкИёЕуЩЯЃЌЕуBЕФзјБъЮЊЃЈ1ЃЌ0ЃЉЃЎ
ЃЈ1ЃЉЛГіЁїABCЙигкxжсЖдГЦЕФЁїA1B1C1ЃЛ
ЃЈ2ЃЉЛГіНЋЁїABCШЦдЕуOАДФцЪБеыа§зЊ90ЁуЫљЕУЕФЁїA2B2C2ЃЌВЂаДГіЕуC2ЕФзјБъЃЛ
ЃЈ3ЃЉЁїA1B1C1гыЁїA2B2C2ГЩжааФЖдГЦТ№ЃПШєГЩжааФЖдГЦЃЌаДГіЖдГЦжааФЕФзјБъЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
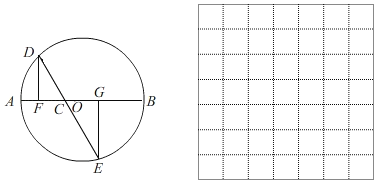
ЁОЬтФПЁПШчЭМЃЌABЪЧЁбOЕФжБОЖЃЌAB=4cmЃЌCЮЊABЩЯвЛЖЏЕуЃЌЙ§ЕуCЕФжБЯпНЛЁбOгкDЁЂEСНЕуЃЌЧвЁЯACD=60ЁуЃЌDFЁЭABгкЕуFЃЌEGЁЭABгкЕуGЃЌЕБЕуCдкABЩЯдЫЖЏЪБЃЌЩшAF=xcmЃЌDE=ycm(ЕБxЕФжЕЮЊ0Лђ3ЪБЃЌyЕФжЕЮЊ2)ЃЌЬНОПКЏЪ§yЫцздБфСПxЕФБфЛЏЖјБфЛЏЕФЙцТЩЃЎ
ЃЈ1ЃЉЭЈЙ§ШЁЕуЁЂЛЭМЁЂВтСПЃЌЕУЕНСЫxгыyЕФМИзщЖдгІжЕЃЌШчЯТБэЃК
x/cm | 0 | 0.40 | 0.55 | 1.00 | 1.80 | 2.29 | 2.61 | 3 |
y/cm | 2 | 3.68 | 3.84 | 3.65 | 3.13 | 2.70 | 2 |
ЃЈ2ЃЉНЈСЂЦНУцжБНЧзјБъЯЕЃЌУшГівдВЙШЋКѓЕФБэжаИїЖдЖдгІжЕЮЊзјБъЕФЕуЃЌЛГіИУКЏЪ§ЕФЭМЯѓЃЛ
ЃЈ3ЃЉНсКЯЛГіЕФКЏЪ§ЭМЯѓЃЌНтОіЮЪЬтЃКЕуFгыЕуOжиКЯЪБЃЌDEГЄЖШдМЮЊЁЁЁЁЁЁЁЁcm(НсЙћБЃСєвЛЮЛаЁЪ§)ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
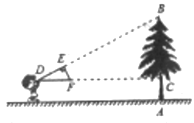
ЁОЬтФПЁПШчЭМЃЌаЁУїЭЌбЇгУзджЦЕФжБНЧШ§НЧаЮжНАхDEFВтСПЪїЕФИпЖШABЃЌЫћЕїећздМКЕФЮЛжУЃЌЩшЗЈЪЙаББпDFБЃГжЫЎЦНЃЌВЂЧвБпDEгыЕуBдкЭЌвЛжБЯпЩЯЃЌвбжЊжНАхЕФСНЬѕжБНЧБпDE=0.4mЃЌEF=0.2mЃЌВтЕУБпDFРыЕиУцЕФИпЖШAC=1.5mЃЌCD=8mЃЌЧѓЪїИпЁЃ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
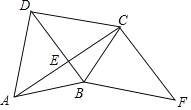
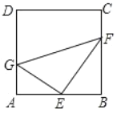
ЁОЬтФПЁПШчЭМЃЌЫФБпаЮABCDЕФЖдНЧЯпACЁЭBDгкЕуEЃЌABЃНBCЃЌFЮЊЫФБпаЮABCDЭтвЛЕуЃЌЧвЁЯFCAЃН90ЁуЃЌЁЯCBFЃНЁЯDCBЃЎ
ЃЈ1ЃЉЧѓжЄЃКЫФБпаЮDBFCЪЧЦНааЫФБпаЮЃЛ
ЃЈ2ЃЉШчЙћBCЦНЗжЁЯDBFЃЌЁЯFЃН45ЁуЃЌBDЃН2ЃЌЧѓACЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
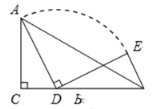
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌЁЯACB 90ЃЌAC3ЃЌCB5ЃЌЕуDЪЧCBБпЩЯЕФвЛИіЖЏЕуЃЌНЋЯпЖЮADШЦзХЕуD ЫГЪБеыа§зЊ90ЃЌЕУЕНЯпЖЮDEЃЌСЌНсBEЃЌдђЯпЖЮBEЕФзюаЁжЕЕШгк__________ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдке§ЗНаЮ![]() жаЃЌ
жаЃЌ![]() ЮЊ
ЮЊ![]() БпЕФжаЕуЃЌ
БпЕФжаЕуЃЌ![]() ЁЂ
ЁЂ![]() ЗжБ№ЮЊ
ЗжБ№ЮЊ![]() ЁЂ
ЁЂ![]() БпЩЯЕФЕуЃЌШє
БпЩЯЕФЕуЃЌШє![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌдђ
ЃЌдђ![]() ЕФГЄЮЊЃЈ ЃЉ
ЕФГЄЮЊЃЈ ЃЉ
A.2B.3C.![]() D.
D.![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
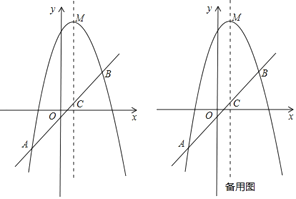
ЁОЬтФПЁПвбжЊЃЌШчЭМЃЌХзЮяЯп![]() ЕФЖЅЕуЮЊ
ЕФЖЅЕуЮЊ![]() ЃЌОЙ§ХзЮяЯпЩЯЕФСНЕу
ЃЌОЙ§ХзЮяЯпЩЯЕФСНЕу![]() КЭ
КЭ![]() ЕФжБЯпНЛХзЮяЯпЕФЖдГЦжсгкЕу
ЕФжБЯпНЛХзЮяЯпЕФЖдГЦжсгкЕу![]() ЃЎ
ЃЎ
ЃЈ1ЃЉЧѓХзЮяЯпЕФНтЮіЪНКЭжБЯп![]() ЕФНтЮіЪНЃЎ
ЕФНтЮіЪНЃЎ
ЃЈ2ЃЉдкХзЮяЯпЩЯ![]() СНЕужЎМфЕФВПЗжЃЈВЛАќКЌ
СНЕужЎМфЕФВПЗжЃЈВЛАќКЌ![]() СНЕуЃЉЃЌЪЧЗёДцдкЕу
СНЕуЃЉЃЌЪЧЗёДцдкЕу![]() ЃЌЪЙЕУ
ЃЌЪЙЕУ![]() ЃПШєДцдкЃЌЧѓГіЕу
ЃПШєДцдкЃЌЧѓГіЕу![]() ЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЃЈ3ЃЉШєЕу![]() дкХзЮяЯпЩЯЃЌЕу
дкХзЮяЯпЩЯЃЌЕу![]() дк
дк![]() жсЩЯЃЌЕБвдЕу
жсЩЯЃЌЕБвдЕу![]() ЮЊЖЅЕуЕФЫФБпаЮЪЧЦНааЫФБпаЮЪБЃЌжБНгаДГіТњзуЬѕМўЕФЕу
ЮЊЖЅЕуЕФЫФБпаЮЪЧЦНааЫФБпаЮЪБЃЌжБНгаДГіТњзуЬѕМўЕФЕу![]() ЕФзјБъЃЎ
ЕФзјБъЃЎ
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com