
如图,抛物线 交y轴于点A,交x轴正半轴于点B.
交y轴于点A,交x轴正半轴于点B.
(1)求直线AB对应的函数关系式;
(2)有一宽度为1的直尺平行于x轴,在点A、B之间平行移动,直尺两长边所在直线被直线AB和抛物线截得两线段MN、PQ,设M点的横坐标为m,且0<m<3.试比较线段MN与PQ的大小.
(1)y=2x﹣8
(2)①当2m﹣3<0,即0<m<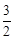 时, 则MN﹣PQ<0,即MN<PQ;
时, 则MN﹣PQ<0,即MN<PQ;
②当2m﹣3=0,即m=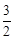 时, 则MN﹣PQ=0,即MN=PQ;
时, 则MN﹣PQ=0,即MN=PQ;
③当2m﹣3>0即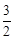 <m<3时,则MN﹣PQ>0,即MN>PQ。
<m<3时,则MN﹣PQ>0,即MN>PQ。
解析分析:(1)利用二次函数解析式,求出A、B两点的坐标,再利用待定系数法求出一次函数解析式;
(2)根据M的横坐标和直尺的宽度,求出P的横坐标,再代入直线和抛物线解析式,求出MN、PQ的长度表达式,再比较即可。
解:(1)当x=0时,y=﹣8;
当y=0时,x2﹣2x﹣8=0,解得,x1=4,x2=﹣8。
∴A(0,﹣8),B(4,0)。
设一次函数解析式为y=kx+b,
将A(0,﹣8),B(4,0)分别代入解析式得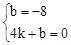 ,解得,
,解得,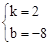 。
。
∴一次函数解析式为y=2x﹣8。
(2)∵M点横坐标为m,则P点横坐标为(m+1)。
∴ ;
;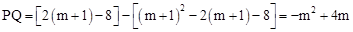 。
。
∴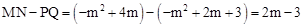 。
。
∵0<m<3,
∴①当2m﹣3<0,即0<m<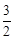 时, 则MN﹣PQ<0,即MN<PQ;
时, 则MN﹣PQ<0,即MN<PQ;
②当2m﹣3=0,即m=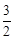 时, 则MN﹣PQ=0,即MN=PQ;
时, 则MN﹣PQ=0,即MN=PQ;
③当2m﹣3>0即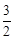 <m<3时,则MN﹣PQ>0,即MN>PQ。
<m<3时,则MN﹣PQ>0,即MN>PQ。


 考前必练系列答案
考前必练系列答案科目:初中数学 来源: 题型:解答题
某商场经营某种品牌的玩具,购进时的单价是30元,根据市场调查:在一段时间内,销售单价是40元时,销售量是600件,而销售单价每涨1元,就会少售出10件玩具.
(1)不妨设该种品牌玩具的销售单价为x元(x>40),请你分别用x的代数式来表示销售量y件和销售该品牌玩具获得利润w元,并把结果填写在表格中:
| 销售单价(元) | x |
| 销售量y(件) | |
| 销售玩具获得利润w(元) | |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,平面直角坐标系中,以点C(2, )为圆心,以2为半径的圆与x轴交于A,B两点.
)为圆心,以2为半径的圆与x轴交于A,B两点.
(1)求A,B两点的坐标;
(2)若二次函数y=x2+bx+c的图象经过点A,B,试确定此二次函数的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
2011年11月28日至12月9日,联合国气候变化框架公约第17次缔约方会议在南非德班召开,大会通过了“德班一揽子决议”(DurbanPackageOutcome),建立德班增强行动平台特设工作组,决定实施《京都议定书》第二承诺期并启动绿色气候基金,中国的积极态度赢得与会各国的尊重.
在气候对人类生存压力日趋加大的今天,发展低碳经济,全面实现低碳生活逐渐成为人们的共识.某企业采用技术革新,节能减排.从去年1至6月,该企业二氧化碳排放量y1(吨)与月份x(1≤x≤6,且x取整数)之间的函数关系如下表:
| 月份x(月) | 1 | 2 | 3 | 4 | 5 | 6 |
| 二氧化碳排放量y1(吨) | 600 | 300 | 200 | 150 | 120 | 100 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
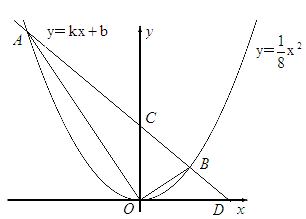
如图,直线 与抛物线
与抛物线 相交于A
相交于A ,B
,B 两点,与x轴正半轴相交于点D,与y轴相交于点C,设△OCD的面积为S,且
两点,与x轴正半轴相交于点D,与y轴相交于点C,设△OCD的面积为S,且 。
。
(1)求b的值;
(2)求证:点 在反比例函数
在反比例函数 的图象上;
的图象上;
(3)求证: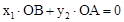 。
。
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
某高中学校为高一新生设计的学生单人桌的抽屉部分是长方体形.其中,抽屉底面周长为180cm,高为20cm.请通过计算说明,当底面的宽x为何值时,抽屉的体积y最大?最大为多少?(材质及其厚度等暂忽略不计).
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,在平面直角坐标系中,二次函数 的图象与
的图象与 轴交于A(
轴交于A( ,0),B(2,0),且与
,0),B(2,0),且与 轴交于点C.
轴交于点C.

(1)求该抛物线的解析式,并判断△ABC的形状;
(2)点P是x轴下方的抛物线上一动点, 连接PO,PC,
并把△POC沿CO翻折,得到四边形 ,求出使四边形
,求出使四边形 为菱形的点P的坐标;
为菱形的点P的坐标;
(3) 在此抛物线上是否存在点Q,使得以A,C,B,Q四点为顶点的四边形是直角梯形?若存在, 求出Q点的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:单选题
点(﹣1,y1),(2,y2),(3,y3)均在函数y= 的图象上,则y1,y2,y3的大小关系是( )
的图象上,则y1,y2,y3的大小关系是( )
| A.y3<y2<y1 | B.y2<y3<y1 |
| C.y1<y2<y3 | D.y1<y3<y2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com