
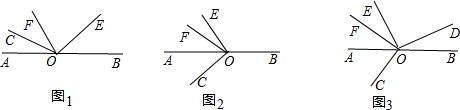
分析 (1)由题意可知:∠FOE=90°-∠COF,由角平分线的性质可求得∠AOE=2∠EOF,所以∠BOE=180°-∠AOE,即可求得答案.
(2)设∠COF=n°,故∠EOF=90°-n,由角平分线的性质即可求得∠AOE=180°-2n°,从而求得∠BOE与∠COF的数量关系.
(3)由(2)可知:∠BOE=2∠COF=130°,进而求得∠AOE=180°-∠BOE=50°,由于OF平分∠AOE,所以∠AOF=$\frac{1}{2}$∠AOE=25°,分别代入2∠BOD+∠AOF=$\frac{1}{2}$(∠BOE-∠BOD)解得∠BOD即可
解答 解:(1)∵∠COE是直角,∠COF=28°,
∴∠EOF=90°-∠COF=62°,
∵OF平分∠AOE,
∴∠AOE=2∠EOF=124°,
∴∠BOE=180°-∠AOE=56°
若∠COF=n°,
∴∠BOE=2n°,
∴∠BOE=2∠COF,
(2)设∠COF=n°,
∴∠EOF=90°-∠COF=90°-n°,
∵OF平分∠AOE,
∴∠AOE=2∠EOF=180°-2n°,
∴∠BOE=180°-∠AOE=2n°=2∠COF,
故∠BOE与∠COF的关系是仍然成立.
(3)由(2)可知:∠BOE=2∠COF=130°,
∴∠AOE=180°-∠BOE=50°,
∵OF平分∠AOE,
∴∠AOF=$\frac{1}{2}$∠AOE=25°
∵2∠BOD+∠AOF=$\frac{1}{2}$(∠BOE-∠BOD),
∴2∠BOD+25°=$\frac{1}{2}$(130°-∠BOD)
解得:∠BOD=16°
故答案为:(1)56°;2n°;∠BOE=2∠COF
点评 本题考查了角的有关计算和角平分线定义的应用,能表示出各个角之间的关系是解此题的关键.


科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,二次函数y=a(x+1)2+2的图象与x轴交于A,B两点,已知A(-3,0),根据图象回答下列问题.
如图,二次函数y=a(x+1)2+2的图象与x轴交于A,B两点,已知A(-3,0),根据图象回答下列问题.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com