
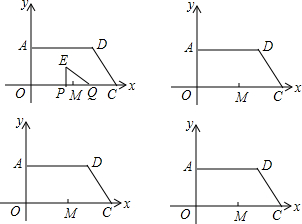
分析 (1)作DH⊥OC于H,如图1,则OH=AD=6,CH=OC-OH=2,再利用特殊角的三角函数值得到∠DCO=60°,然后根据含30度的直角三角形三边的关系得DQ=$\sqrt{3}$CH=2$\sqrt{3}$,于是得到D点坐标为(6,2$\sqrt{3}$);
(2)当点P从点O返回M时,可用t表示出P点坐标为(t-4,0),同时得到Q点坐标为(4+t,0),然后利用两点的横坐标之差计算PQ的长;
(3)分类讨论:当点P从点M向O点运动时,如图1,PE和QE分别交AD于F、G,则MP=OM-OP=2,MQ=MP=2,利用等腰直角三角形的性质得PQ=PE=4,再判断△EFG为等腰直角三角形,得到FG=FE=EP-PF=4-2$\sqrt{3}$,于是△EPQ与梯形AOCD重叠部分的面积S为S梯形FGQP,再根据梯形的面积公式计算即可;当点P从点O向M点运动时,如图2,PE和QE分别交AD于F、G,则PQ=8,同理可得FG=FE=EP-PF=8-2$\sqrt{3}$,由于FD=AD-AF=4,则可判断点D在△PEQ的内部,所以△EPQ与梯形AOCD重叠部分的面积S即为S梯形FDCP,再根据梯形的面积公式计算即可;
(4)当点P运动到点O时,点Q运动到点C,此时AD被覆盖线段的长度达到最大值,t=4,如图3,PE和QE分别交AD于F,则PE=PQ=8,易得FE=AG=8-2$\sqrt{3}$,所以GD=2$\sqrt{3}$-2,所以点P从点O可继续运动(2$\sqrt{3}$-2)秒,FG的长度不变,于是得到此时t的范围为4≤t≤2+2$\sqrt{3}$.
解答 解:(1)作DH⊥OC于H,如图1,则四边形AOHD为矩形,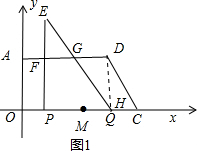
∴OH=AD=6,
∴CH=OC-OH=8-6=2,
∵sin∠DCO=$\frac{\sqrt{3}}{2}$,
∴∠DCO=60°,
在Rt△DCO中,∵∠CDH=30°,
∴DQ=$\sqrt{3}$CH=2$\sqrt{3}$,
∴D点坐标为(6,2$\sqrt{3}$);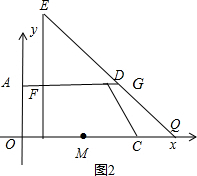
(2)当点P从点O返回M时,P点坐标为(t-4,0),此时Q点坐标为(4+t,0),
∴PQ=4+t-(t-4)=8;
(3)当点P从点M向O点运动时,如图1,PE和QE分别交AD于F、G,则MP=OM-OP=4-2=2,MQ=MP=2,
∵△EPQ为等腰直角三角形,
∴PQ=PE=4,
而FG∥PQ,
∴△EFG为等腰直角三角形,
∴FG=FE=EP-PF=4-2$\sqrt{3}$,
∴△EPQ与梯形AOCD重叠部分的面积S=S梯形FGQP=$\frac{1}{2}$×(4-2$\sqrt{3}$+4)×2$\sqrt{3}$=8$\sqrt{3}$-6;
当点P从点O向M点运动时,如图2,PE和QE分别交AD于F、G,则PQ=8,
∵△EPQ为等腰直角三角形,
∴PQ=PE=8,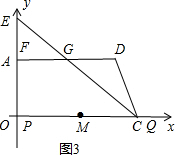
而FG∥PQ,
∴△EFG为等腰直角三角形,
∴FG=FE=EP-PF=8-2$\sqrt{3}$,
而FD=AD-AF=6-2=4,
∴FG>FD,即点D在△PEQ的内部,
∴△EPQ与梯形AOCD重叠部分的面积S=S梯形FDCP=$\frac{1}{2}$×(4+6)×2$\sqrt{3}$=10$\sqrt{3}$;
(4)能.
当点P运动到点O时,点Q运动到点C,此时AD被覆盖线段的长度达到最大值,t=4,如图3,PE和QE分别交AD于F,则PE=PQ=8,
∴FE=AG=8-2$\sqrt{3}$,
∴GD=6-(8-2$\sqrt{3}$)=2$\sqrt{3}$-2,
∴当G点向右运动(2$\sqrt{3}$-2)个单位时,FG的长度不变,
即点P从点O可继续运动(2$\sqrt{3}$-2)秒,FG的长度不变,
∴当4≤t≤4+2$\sqrt{3}$-2,即4≤t≤2+2$\sqrt{3}$时,线段AD会有一部分被△EPQ覆盖,被覆盖线段的长度的最大值能持续一段时间.
点评 本题考查了四边形的综合题:熟练掌握梯形的性质和等腰直角三角形的性质;学会利用代数式法解决动点的问题;注意分类讨论思想的意义.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在扇形OAB中,∠AOB=90°,半径OA=6.将扇形OAB沿过点B的直线折叠.点 O恰好落在延长线上点D处,折痕交OA于点C,整个阴影部分的面积9π-12$\sqrt{3}$.
如图,在扇形OAB中,∠AOB=90°,半径OA=6.将扇形OAB沿过点B的直线折叠.点 O恰好落在延长线上点D处,折痕交OA于点C,整个阴影部分的面积9π-12$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| x | … | -3 | -2 | -1 | 0 | 1 | … |
| y | … | -10 | -4 | 0 | 2 | 2 | … |
| A. | 抛物线的对称轴为x=$\frac{1}{2}$ | |
| B. | 抛物线与x轴的另一个交点为(2,0) | |
| C. | 抛物线与直线y=2的两个交点之间的距离为1 | |
| D. | 在对称轴右侧,y随x增大而增大 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com