
如图7,正方形ABCD的对角线相交于点O,∠CAB的平分线分别交BD、BC于E、F,作BH⊥AF于点H,分别交AC、CD于点G、P,连结GE、GF.
(1)求证:△OAE ≌△OBG.
(2)试问:四边形BFGE是否为菱形?若是,请证明;若不是,请说明理由.
(3)试求: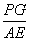 的值(结果保留根号).
的值(结果保留根号).
 |
.解:(1)证明:
∵四边形ABCD是正方形
∴OA=OB,∠AOE=∠BOG=90°
 ∵BH⊥AF
∵BH⊥AF
∴∠AHG=90°
∴∠GAH+∠AGH=90°=∠OBG+∠AGH
∴∠GAH=∠OBG
∴△OAE≌△OBG.
(2)四边形BFGE是菱形,理由如下:
∵∠GAH=∠BAH,AH=AH, ∠AHG=∠AHB
∴△AHG≌△AHB
∴GH=BH
∴AF是线段BG的垂直平分线
∴EG=EB,FG=FB
∵∠BEF=∠BAE+∠ABE= ,∠BFE=90°-∠BAF=67.5°
,∠BFE=90°-∠BAF=67.5°
∴∠BEF=∠BFE
∴EB=FB
∴EG=EB=FB=FG
∴四边形BFGE是菱形
(3)设OA=OB=OC=a,菱形GEBF的边长为b.
∵四边形BFGE是菱形,
∴GF∥OB, ∴∠CGF=∠COB=90°,
∴∠GFC=∠GCF=45°,
∴CG=GF=b
(也可由△OAE≌△OBG得OG=OE=a-b,OC-CG=a-b,得CG=b)
∴OG=OE=a-b,在Rt△GOE中,由勾股定理可得: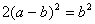 ,求得
,求得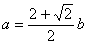
∴AC= ,AG=AC-CG=
,AG=AC-CG=
∵PC∥AB, ∴△CGP∽△AGB,
∴ ,
,
由(1)△OAE≌△OBG得AE=GB,
∴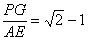


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
已知两点P1(x1,y1)、P2(x2,y2)在函数y=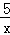 的图象上,当x1>x2>0时,下列结论正确的是( )
的图象上,当x1>x2>0时,下列结论正确的是( )
A. 0<y1<y2 B.0<y2<y1 C. y1<y2<0 D. y2<y1<0


查看答案和解析>>
科目:初中数学 来源: 题型:
某市区一条主要街道的改造工程有甲、乙两个工程队投标.经测算:若由两个工程队合做,12天恰好完成;若两个队合做9天后,剩下的由甲队单独完成,还需5天时间,现需从这两个工程队中选出一个队单独完成,从缩短工期角度考虑,你认为应该选择哪个队?为什么?


查看答案和解析>>
科目:初中数学 来源: 题型:
一个不透明的袋子中有3个分别标有数字3, 1,-2的球,这些球除所标的数字不同外其它都相同.若从袋子中随机摸出两个球,则这两个球上的两个数字之和为负数的概率是( ) A. B.
B.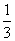 C.
C. D.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
我市某校举办“行为规范在身边”演讲比赛中,7位评委给其中一名选手的评分(单位:分)分别为:9.25,9.82,9.45,9.63,9.57,9.35,9.78.则这组数据的中位数和平均数分别是( )
|
| A. | 9.63和9.54 | B. | 9.57和9.55 | C. | 9.63和9.56 | D. | 9.57和9.57 |


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com