
【题目】如图,在平面直角坐标系中,A(﹣1,5),B(﹣1,0),C(﹣4,3).

(1)请画出△ABC关于y轴对称的△DEF(其中D,E,F分别是A,B,C的对应点,不写画法);
(2)直接写出D,E,F三点的坐标:D( ),E( ),F( );
(3)在y轴上存在一点,使PC﹣PB最大,则点P的坐标为 .
【答案】(1)如图,△DEF即为所求作三角形;见解析;(2)点D(1,5)、E(1,0)、F(4,3);(3)点P坐标为(0,﹣1),
【解析】
(1)分别作出点A、B、C关于y轴对称点D、E、F,即可得△DEF;
(2)根据(1)中图形可得坐标;
(3)延长CB交y轴于P,点P即为所求,待定系数法求直线BC所在直线解析式,即可知其与y轴的交点P的坐标.
(1)如图,△DEF即为所求作三角形;
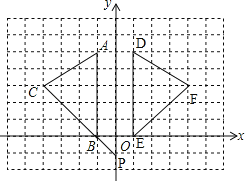
(2)由图可知点D(1,5)、E(1,0)、F(4,3),
故答案为:1,5;1,0;4,3;
(3)延长CB交y轴于P,此时PC﹣PB最大,故点P即为所求,
设BC所在直线解析式为y=kx+b,
将点B(﹣1,0)、点C(﹣4,3)代入,得:![]() ,
,
解得:![]() ,
,
∴直线BC所在直线解析式为y=﹣x﹣1,
当x=0时,y=﹣1,
∴点P坐标为(0,﹣1),
故答案为:(0,﹣1).


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
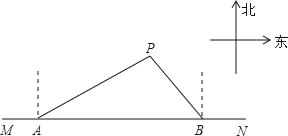
【题目】如图,在东西方向的海岸线MN上有A,B两艘船,船长都收到已触礁搁浅的船P的求救信号,已知船P在船A的北偏东60°方向36海里处,船P在船B顶点北偏西37°方向,若船A,船B分别以30海里/小时,20海里/小时的速度同时出发,匀速前往救援,通过计算判断哪艘船先到达船P处.(参考数据![]() =1.73,sin37°=0.6,cos37°=0.80)
=1.73,sin37°=0.6,cos37°=0.80)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,AB=10,AC=8.线段AD由线段AB绕点A按逆时针方向旋转90°得到,△EFG由△ABC沿CB方向平移得到,且直线EF过点D.
(1)求∠BDF的大小;
(2)求CG的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在学习过程中,对教材中的一个有趣问题做如下探究:

(习题回顾)已知:如图1,在△ABC中,∠ACB=90°,AE是角平分线,CD是高,AE、CD相交于点F.求证:∠CFE=∠CEF;
(变式思考)如图2,在△ABC中,∠ACB=90°,CD是AB边上的高,若△ABC的外角∠BAG的平分线交CD的延长线于点F,其反向延长线与BC边的延长线交于点E,则∠CFE与∠CEF还相等吗?说明理由;
(探究廷伸)如图3,在△ABC中,在AB上存在一点D,使得∠ACD=∠B,角平分线AE交CD于点F.△ABC的外角∠BAG的平分线所在直线MN与BC的延长线交于点M.试判断∠M与∠CFE的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在△ABC中,∠BAC=130°,AB的垂直平分线ME交BC于点M,交AB于点E,AC的垂直平分线NF交BC于点N,交AC于点F,则∠MAN为( )

A.80°B.70°C.60°D.50°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中.AB=AC.∠BAC=36°.BD是∠ABC的平分线,交AC于点D,E是AB的中点,连接ED并延长,交BC的延长线于点F,连接AF.求证:(1)EF⊥AB; (2)△ACF为等腰三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校从两名优秀选手中选一名参加全市中小学运动会的男子![]() 米跑项目,该校预先对这两名选手测试了
米跑项目,该校预先对这两名选手测试了![]() 次,测试成绩如下表
次,测试成绩如下表
|
|
|
|
|
|
|
| |
甲的成绩(秒) |
|
|
|
|
|
|
|
|
乙的成绩(秒) |
|
|
|
|
|
|
|
|
![]() 为了衡量这两名选手
为了衡量这两名选手![]() 米跑的水平,你选择哪些统计量?请分别求出这些统计量的值.
米跑的水平,你选择哪些统计量?请分别求出这些统计量的值.
![]() 你认为选派谁比较合适?为什么?
你认为选派谁比较合适?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
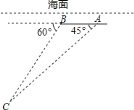
【题目】如图,埃航![]() 客机失事后,国家主席亲自发电进行慰问,埃及政府出动了多艘舰船和飞机进行搜救,其中一艘潜艇在海面下
客机失事后,国家主席亲自发电进行慰问,埃及政府出动了多艘舰船和飞机进行搜救,其中一艘潜艇在海面下![]() 米的
米的![]() 点处测得俯角为
点处测得俯角为![]() 的前下方海底有黑匣子信号发出,继续沿原方向直线航行
的前下方海底有黑匣子信号发出,继续沿原方向直线航行![]() 米后到达
米后到达![]() 点,在
点,在![]() 处测得俯角为
处测得俯角为![]() 的前下方海底有黑匣子信号发出,求海底黑匣子
的前下方海底有黑匣子信号发出,求海底黑匣子![]() 点距离海面的深度(结果保留根号).
点距离海面的深度(结果保留根号).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com