
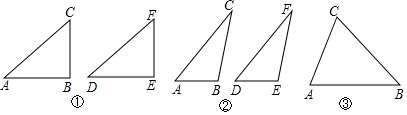
���� ��1������ֱ��������ȫ�ȵķ�����HL��֤����
��2������C��CG��AB��AB���ӳ�����G������F��FH��DE��DE���ӳ�����H�����ݵȽǵIJ�����������CBG=��FEH�������á��ǽDZߡ�֤����CBG�͡�FEHȫ�ȣ�����ȫ�������ζ�Ӧ����ȿɵ�CG=FH�������á�HL��֤��Rt��ACG��Rt��DFHȫ�ȣ�����ȫ�������ζ�Ӧ����ȿɵá�A=��D��Ȼ�����á��ǽDZߡ�֤����ABC�͡�DEFȫ�ȣ�
��3���Ե�CΪԲ�ģ���AC��Ϊ�뾶��������AB�ཻ�ڵ�D��E��B�غϣ�F��C�غϣ��õ���DEF���ABC��ȫ�ȣ�
��� ��1���⣺HL��
�ʴ�Ϊ��HL��
��2��֤������ͼ��
����C��CG��AB��AB���ӳ�����G������F��FH��DE��DE���ӳ�����H��
�ߡ�ABC=��DEF���ҡ�ABC����DEF���Ƕ۽ǣ�
��180��-��ABC=180��-��DEF��
����CBG=��FEH��
�ڡ�CBG�͡�FEH�У�$\left\{\begin{array}{l}{��CBG=��FEH}\\{��G=��H=90��}\\{BC=EF}\end{array}\right.$
���CBG�ա�FEH��AAS����
��CG=FH��
��Rt��ACG��Rt��DFH��$\left\{\begin{array}{l}{AC=DF}\\{CG=FH}\end{array}\right.$
��Rt��ACG��Rt��DFH��HL����
���A=��D��
�ڡ�ABC�͡�DEF�У�$\left\{\begin{array}{l}{��A=��D}\\{��ABC=��DEF}\\{AC=DF}\end{array}\right.$
���ABC�ա�DEF��AAS����
��3���⣺��ͼ����DEF�͡�ABC��ȫ�ȣ�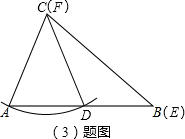
�Ե�CΪԲ�ģ���AC��Ϊ�뾶��������AB�ཻ�ڵ�D��E��B�غϣ�F��C�غϣ��õ���DEF���ABC��ȫ�ȣ�
���� �������������ۺ��⣬��Ҫ������ȫ�������ε��ж������ʣ�Ӧ���������ͼ����������������ȫ�ȵ��ж������ǽ���Ĺؼ����Ķ����ϴ�����Ҫ������ϸ��


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ����ABCD�У��Խ���AC��BD�ཻ��O����AOB=60�㣬AC=10��
����ABCD�У��Խ���AC��BD�ཻ��O����AOB=60�㣬AC=10���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com