
【题目】如图,在正方形ABCD中,P是边BC上的一动点(不与点B,C重合),点B关于直线AP的对称点为E,连接AE,连接DE并延长交射线AP于点F,连接BF
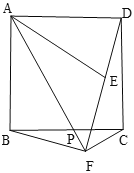
(1)若![]() ,直接写出
,直接写出![]() 的大小(用含
的大小(用含![]() 的式子表示).
的式子表示).
(2)求证:![]() .
.
(3)连接CF,用等式表示线段AF,BF,CF之间的数量关系,并证明.
【答案】(1)45°+![]() ;(2)证明见解析;(3)AF=
;(2)证明见解析;(3)AF=![]() BF+CF.
BF+CF.
【解析】
(1)过点A作AG⊥DF于G,由轴对称性质和正方形的性质可得AE=AD,∠BAP=∠EAF,根据等腰三角形“三线合一”的性质可得∠EAG=∠DAG,即可得∠FAG=![]() ∠BAD=45°,∠DAG+∠BAP=45°,根据直角三角形两锐角互余的性质即可得答案;
∠BAD=45°,∠DAG+∠BAP=45°,根据直角三角形两锐角互余的性质即可得答案;
(2)由(1)可得∠FAG=![]() ∠BAD=45°,由AG⊥PD可得∠APG=45°,根据轴对称的性质可得∠BPA=∠APG=45°,可得∠BFD=90°,即可证明BF⊥DF;
∠BAD=45°,由AG⊥PD可得∠APG=45°,根据轴对称的性质可得∠BPA=∠APG=45°,可得∠BFD=90°,即可证明BF⊥DF;
(3)连接BD、BE,过点C作CH//FD,交BE延长线于H,由∠BFD=∠BCD=90°可得B、F、C、D四点共圆,根据圆周角定理可得∠FBC=∠FDC,∠DFC=∠DBC=45°,根据平行线的性质可得∠FDC=∠DCH,根据角的和差关系可得∠ABF=∠BCH,由轴对称性质可得BF=EF,可得△BEF是等腰直角三角形,即可得∠BEF=45°,BE=![]() BF,即可证明∠BEF=∠DFC,可得BH//FC,即可证明四边形EFCH是平行四边形,可得EH=FC,EF=CH,利用等量代换可得CH=BF,利用SAS可证明△ABF≌△BCH,可得AF=BH,即可得AF、BF、CF的数量关系.
BF,即可证明∠BEF=∠DFC,可得BH//FC,即可证明四边形EFCH是平行四边形,可得EH=FC,EF=CH,利用等量代换可得CH=BF,利用SAS可证明△ABF≌△BCH,可得AF=BH,即可得AF、BF、CF的数量关系.
(1)过点A作AG⊥DF于G,
∵点B关于直线AF的对称点为E,四边形ABCD是正方形,
∴AE=AB,AB=AD=DC=BC,∠BAF=∠EAF,
∴AE=AD,
∵AG⊥FD,
∴∠EAG=∠DAG,
∴∠BAF+∠DAG=∠EAF+∠EAG,
∵∠BAF+∠DAG+∠EAF+∠EAG=∠BAD=90°,
∴∠BAF+∠DAG=∠GAF=45°,
∴∠DAG=45°-![]() ,
,
∴∠ADF=90°-∠DAG=45°+![]() .
.
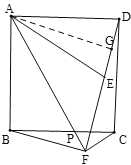
(2)由(1)得∠GAF=45°,
∵AG⊥FD,
∴∠AFG=45°,
∵点E、B关于直线AF对称,
∴∠AFB=∠AFE=45°,
∴∠BFG=90°,
∴BF⊥DF.
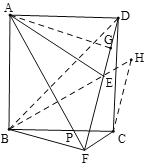
(3)连接BD、BE,过点C作CH//FD,交BE延长线于H,
∵∠BFD=∠BCD=90°,
∴B、F、C、D四点共圆,
∴∠FDC=∠FBC,∠DFC=∠DBC=45°,
∵CH//FD,
∴∠DCH=∠FDC,
∴∠FBC=∠DCH,
∵∠ABC=∠BCD=90°,
∴∠ABC+∠FBC=∠BCD+∠DCH,即∠ABF=∠BCH,
∵点E、B关于直线AF对称,
∴BF=EF,
∵∠BFE=90°,
∴△BEF是等腰直角三角形,
∴∠BEF=45°,BE=![]() BF,
BF,
∴∠BEF=∠DFC,
∴FC//BH,
∴四边形EFCH是平行四边形,
∴EH=FC,CH=BF,
在△ABF和△BCH中,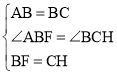 ,
,
∴AF=BH=BE+EH=![]() BF+CF.
BF+CF.


科目:初中数学 来源: 题型:
【题目】弹簧原长(不挂重物)15cm,弹簧总长L(cm)与重物质量x(kg)的关系如下表所示:
弹簧总长L(cm) | 16 | 17 | 18 | 19 | 20 |
重物重量x(kg) | 0.5 | 1.0 | 1.5 | 2.0 | 2.5 |
当重物质量为5kg(在弹性限度内)时,弹簧总长L(cm)是( )
A.22.5B.25C.27.5D.30
查看答案和解析>>
科目:初中数学 来源: 题型:
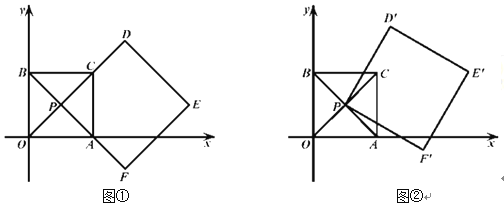
【题目】如图①,在平面直角坐标系中,四边形![]() 是正方形,点
是正方形,点![]() 为正方形
为正方形![]() 对角线的交点,点
对角线的交点,点![]() ,点
,点![]() ,点
,点![]() .分别延长
.分别延长![]() 到
到![]() ,
,![]() 到
到![]() ,使
,使![]() ,
,![]() ,再以
,再以![]() ,
,![]() 为邻边作平行四边形
为邻边作平行四边形![]() .
.
(Ⅰ)求点![]() 的坐标;
的坐标;
(Ⅱ)如图②,将四边形![]() 绕点
绕点![]() 逆时针旋转得四边形
逆时针旋转得四边形![]() ,点
,点![]() ,
,![]() ,
,![]() 旋转后的对应点分别为
旋转后的对应点分别为![]() ,
,![]() ,
,![]() ,旋转角为
,旋转角为![]() .
.
①旋转过程中,当![]() 时,求点
时,求点![]() 的坐标;
的坐标;
②在旋转过程中,求![]() 的取值范围(直接写出结果即可).
的取值范围(直接写出结果即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年由于防控疫情,师生居家隔离线上学习,AB和CD是社区两栋邻楼的示意图,小华站在自家阳台的C点,测得对面楼顶点A的仰角为30°,地面点E的俯角为45°.点E在线段BD上.测得B,E间距离为8.7米.楼AB高12![]() 米.求小华家阳台距地面高度CD的长(结果精确到1米,
米.求小华家阳台距地面高度CD的长(结果精确到1米,![]() 1.41,
1.41,![]() 1.73)
1.73)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】ABCD中,E是CD边上一点,
(1)将△ADE绕点A按顺时针方向旋转,使AD、AB重合,得到△ABF,如图1所示.观察可知:与DE相等的线段是 ,∠AFB=∠
(2)如图2,正方形ABCD中,P、Q分别是BC、CD边上的点,且∠PAQ=45°,试通过旋转的方式说明:DQ+BP=PQ;
(3)在(2)题中,连接BD分别交AP、AQ于M、N,你还能用旋转的思想说明BM2+DN2=MN2吗?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着地铁和共享单车的发展,“地铁+单车”已成为很多市民出行的选择.李华从文化宫站出发,先乘坐地铁,准备在离家较近的A,B,C,D,E中的某一站出地铁,再骑共享单车回家.设他出地铁的站点与文化宫站的距离为![]() (单位:km),乘坐地铁的时间
(单位:km),乘坐地铁的时间![]() (单位:min)是关于
(单位:min)是关于![]() 的一次函数,其关系如下表:
的一次函数,其关系如下表:
地铁站 | A | B | C | D | E |
x/km | 7 | 9 | 11 | 12 | 13 |
y1/min | 16 | 20 | 24 | 26 | 28 |
(1)求![]() 关于
关于![]() 的函数解析式;
的函数解析式;
(2)李华骑单车的时间![]() (单位:min)也受
(单位:min)也受![]() 的影响,其关系可以用
的影响,其关系可以用![]() =
=![]()
![]() 2-11
2-11![]() +78来描述.求李华应选择在哪一站出地铁,才能使他从文化宫站回到家所需的时间最短,并求出最时间.
+78来描述.求李华应选择在哪一站出地铁,才能使他从文化宫站回到家所需的时间最短,并求出最时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,某社会实践活动小组实地测量两岸互相平行的一段河的宽度,在河的南岸边点A处,测得河的北岸边点B在其北偏东45°方向,然后向西走60 m到达点C,测得点B在点C的北偏东60°方向,如图②.
(1)求∠CBA的度数;
(2)求出这段河的宽(结果精确到1 m,参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73).
≈1.73).

① ②
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com