
分析 (1)根据角平分线的定义和角的和差即可得到结论;
(2)方法同(1);
(3)方法同(1).
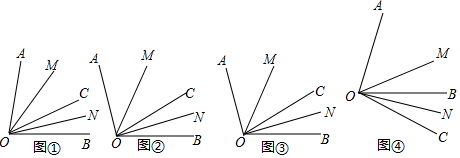
解答 解:(1)∵OM,ON分别是∠AOC和∠BOC的角平分线,
∴∠COM=$\frac{1}{2}∠$AOC=25°,∠CON=$\frac{1}{2}∠$BOC=15°,
∴∠MON=∠MOC+∠NOC=40°,
故答案为:40°;
(2)∵∠AOB=100°,∠BOC=30°,
∴∠AOC=∠AOB-∠BOC=70°,
∵OM,ON分别是∠AOC和∠BOC的角平分线,
∴∠COM=$\frac{1}{2}∠$AOC=35°,∠CON=$\frac{1}{2}∠$BOC=15°,
∴∠MON=∠MOC+∠NOC=50°,
故答案为:50°;
(3)探究一:如图③,当射线OC位于∠AOB内部时,∠MON=$\frac{1}{2}$∠AOB,
证明:∵OM,ON分别是∠AOC和∠BOC的角平分线,
∴∠COM=$\frac{1}{2}∠$AOC=25°,∠CON=$\frac{1}{2}∠$BOC=15°,
∴∠MON=∠MOC+∠NOC=$\frac{1}{2}$(∠AOC+∠BOC)=$\frac{1}{2}∠$AOB;
探究二:如图④,当射线OC位于∠AOB外部时,∠MON=$\frac{1}{2}$∠AOB,
证明:∵OM,ON分别是∠AOC和∠BOC的角平分线,
∴∠COM=$\frac{1}{2}∠$AOC=25°,∠CON=$\frac{1}{2}∠$BOC=15°,
∴∠MON=∠MOC-∠NOC=$\frac{1}{2}$(∠AOC-∠BOC)=$\frac{1}{2}∠$AOB.
点评 本题主要考查了角平分线的定义,解题的关键是利用了角平分线的定义和图中各角之间的和差关系,难度中等.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
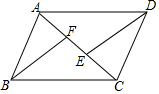 如图,在四边形ABCD中,AD∥BC,点E,F在对角线AC上,且AE=CF,∠ADE=∠CBF.不添加字母及辅助线,写出图中两对全等三角形,并选一对进行证明.
如图,在四边形ABCD中,AD∥BC,点E,F在对角线AC上,且AE=CF,∠ADE=∠CBF.不添加字母及辅助线,写出图中两对全等三角形,并选一对进行证明.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
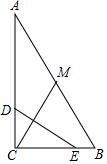 如图,在Rt△ABC中,点D、E分别在AC、BC上,将△CDE沿直线DE翻折,点C恰好落在斜边AB的中点M处.
如图,在Rt△ABC中,点D、E分别在AC、BC上,将△CDE沿直线DE翻折,点C恰好落在斜边AB的中点M处.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
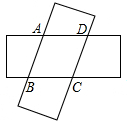 如图用两个完全相同的1cm×4cm长方形纸片,其中心用细铁丝串起来,使纸片交叉叠合,旋转纸片,保持重叠部分形状为菱形,则菱形的最大面积是$\frac{17}{8}$cm2.
如图用两个完全相同的1cm×4cm长方形纸片,其中心用细铁丝串起来,使纸片交叉叠合,旋转纸片,保持重叠部分形状为菱形,则菱形的最大面积是$\frac{17}{8}$cm2.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com