
【题目】将矩形ABCD折叠使A,C重合,折痕交BC于E,交AD于F,

(1)求证:四边形AECF为菱形;
(2)若AB=4,BC=8,求菱形的边长;
(3)在(2)的条件下折痕EF的长.
【答案】(1)见试题解析(2)5(3)2![]() .
.
【解析】
试题(1)根据折叠的性质得OA=OC,EF⊥AC,EA=EC,再利用AD∥AC得到∠FAC=∠ECA,则可根据“ASA”判断△AOF≌△COE,得到OF=OE,加上OA=OC,AC⊥EF,于是可根据菱形的判定方法得到四边形AECF为菱形;
(2)设菱形的边长为x,则BE=BC﹣CE=8﹣x,AE=x,在Rt△ABE中根据勾股定理得(8﹣x)2+42=x2,然后解方程即可得到菱形的边长;
(3)先在Rt△ABC中,利用勾股定理计算出AC=4![]() ,则OA=
,则OA=![]() AC=2
AC=2![]() ,然后在Rt△AOE中,利用勾股定理计算出OE=
,然后在Rt△AOE中,利用勾股定理计算出OE=![]() ,所以EF=2OE=2
,所以EF=2OE=2![]() .
.
试题解析:(1)证明:∵矩形ABCD折叠使A,C重合,折痕为EF,∴OA=OC,EF⊥AC,EA=EC,
∵AD∥AC,∴∠FAC=∠ECA,在△AOF和△COE中,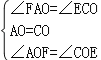 ,∴△AOF≌△COE,
,∴△AOF≌△COE,
∴OF=OE,∵OA=OC,AC⊥EF,
∴四边形AECF为菱形;
(2)解:设菱形的边长为x,则BE=BC﹣CE=8﹣x,AE=x,
在Rt△ABE中,∵BE2+AB2=AE2,
∴(8﹣x)2+42=x2,解得x=5,
即菱形的边长为5;
(3)解:在Rt△ABC中,AC=![]() =
=![]() =4
=4![]() ,
,
∴OA=![]() AC=2
AC=2![]() ,
,
在Rt△AOE中,OE=![]() =
=![]() =
=![]() ,
,
∴EF=2OE=2![]() .
.


 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案科目:初中数学 来源: 题型:
【题目】如图,已知∠AOB,以O为圆心,以任意长为半径作弧,分别交OA,OB于F,E两点,再分别以E,F为圆心,大于![]() EF长为半径作圆弧,两条圆弧交于点P,作射线OP,过点F作FD∥OB交OP于点D.
EF长为半径作圆弧,两条圆弧交于点P,作射线OP,过点F作FD∥OB交OP于点D.
(1)若∠OFD=116°,求∠DOB的度数;
(2)若FM⊥OD,垂足为M,求证:△FMO≌△FMD.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O分别与BC,AC交于点D,E,过点D作DF⊥AC于点F.
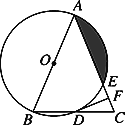
(1)判断DF与是⊙O的位置关系,并证明你的结论。
(2)若⊙O的半径为4,∠CDF=22.5°,求阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一块长和宽分别为60厘米和40厘米的长方形铁皮,要在它的四角截去四个相等的小正方形,折成一个无盖的长方体水槽,使它的底面积为800平方厘米.求截去正方形的边长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学活动 实验、猜想与证明
问题情境
(1)数学活动课上,小颖向同学们提出了这样一个问题:如图(1),在矩形ABCD中,AB=2BC,M、N分别是AB,CD的中点,作射线MN,连接MD,MC,请直接写出线段MD与MC之间的数量关系.

解决问题
(2)小彬受此问题启发,将矩形ABCD变为平行四边形,其中∠A为锐角,如图(2),AB=2BC,M,N分别是AB,CD的中点,过点C作CE⊥AD交射线AD于点E,交射线MN于点F,连接ME,MC,则ME=MC,请你证明小彬的结论;
(3)小丽在小彬结论的基础上提出了一个新问题:∠BME与∠AEM有怎样的数量关系?请你回答小丽提出的这个问题,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
小明在数学课外小组活动时遇到这样一个问题:
![]()
如果一个不等式中含有绝对值,并且绝对值符号中含有未知数,我们把这个不等式叫做绝对值不等式,求绝对值不等式|x|>3的解集.
小明同学的思路如下:
先根据绝对值的定义,求出|x|恰好是3时x的值,并在数轴上表示为点A,B,如图所示.观察数轴发现,以点A,B为分界点把数轴分为三部分:
点A左边的点表示的数的绝对值大于3;
点A,B之间的点表示的数的绝对值小于3;
点B右边的点表示的数的绝对值大于3.
因此,小明得出结论绝对值不等式|x|>3的解集为:x<-3或x>3.
参照小明的思路,解决下列问题:
(1)请你直接写出下列绝对值不等式的解集.
①|x|>1的解集是 .
②|x|<2.5的解集是 .
(2)求绝对值不等式2|x-3|+5>13的解集.
(3)直接写出不等式x2>4的解集是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程 x2-6x+m+4=0有两个实数根 x1,x2.
(1)求m的取值范围;
(2)若 x1,x2满足x2-2x1=-3 ,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:∠1+∠2=180°,∠B=∠D,CD平分∠ACF.
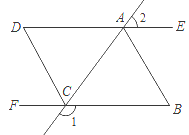
(1)DE与BF平行吗?请说明理由.
(2)AB与CD位置关系如何?为什么?
(3)AB平分∠CAE吗?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com