
 如图,△ABC中,DE∥BC,AN交DE于M,求证:$\frac{DM}{BN}=\frac{EM}{CN}$.
如图,△ABC中,DE∥BC,AN交DE于M,求证:$\frac{DM}{BN}=\frac{EM}{CN}$. 分析 根据平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段成比例,由DM∥BN得到$\frac{DM}{BN}$=$\frac{AM}{AN}$,由ME∥NC得到$\frac{EM}{CN}$=$\frac{AM}{AN}$,然后利用等量代换即可得到结论.
解答 证明:∵DM∥BN,
∴$\frac{DM}{BN}$=$\frac{AM}{AN}$,
∵ME∥NC,
∴$\frac{EM}{CN}$=$\frac{AM}{AN}$,
∴$\frac{DM}{BN}=\frac{EM}{CN}$.
点评 本题考查了平行线分线段成比例:三条平行线截两条直线,所得的对应线段成比例;平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段成比例.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 1 | 2 | 3 | 4 | 5 | 6 |
| 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 |
| 19 | 20 | 21 | 22 | 23 | 24 |
| … | … | … | … | … | … |
| 997 | 998 | 999 | 1000 | 1001 | 1002 |
| … | … | … | … | … | … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
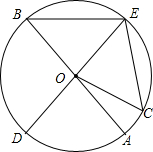 如图,AB,DE是⊙O的直径,C是⊙O上的一点,且$\widehat{AD}$=$\widehat{CE}$.
如图,AB,DE是⊙O的直径,C是⊙O上的一点,且$\widehat{AD}$=$\widehat{CE}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com