
”¾ĢāÄæ”æij³¬ŹŠ¾ö¶Ø¹ŗ½ų¼×”¢ŅŅĮ½ÖÖČ”ÅÆĘ÷£¬ŅŃÖŖ¼×ÖÖČ”ÅÆĘ÷ĆæĢؽų¼Ū±ČŅŅÖÖČ”ÅÆĘ÷¶ą500ŌŖ£¬ ÓĆ40000ŌŖ¹ŗ½ų¼×ÖÖČ”ÅÆĘ÷µÄŹżĮæÓėÓĆ30000ŌŖ¹ŗ½ųŅŅÖÖČ”ÅÆĘ÷µÄŹżĮæĻąĶ¬£®Ēė½ā“šĻĀĮŠĪŹĢā£ŗ
£Ø1£©Ēó¼×”¢ŅŅĮ½ÖÖČ”ÅÆĘ÷ĆæĢصĽų¼Ū£»
£Ø2£©Čō¼×ÖÖČ”ÅÆĘ÷ĆæĢØŹŪ¼Ū2500ŌŖ£¬ŅŅÖÖČ”ÅÆĘ÷ĆæĢØŹŪ¼Ū1800ŌŖ£¬³¬ŹŠÓūĶ¬Ź±¹ŗ½ųĮ½ÖÖČ”ÅÆĘ÷20 ĢØ£¬ĒŅČ«²æŹŪ³ö£®Éč¹ŗ½ų¼×ÖÖČ”ÅÆĘ÷x£ØĢØ£©£¬Ėł»ńĄūČóĪŖy£ØŌŖ£©£¬ŹŌÓĆ¹ŲÓŚxµÄŹ½×Ó±ķŹ¾y£»
£Ø3£©ŌŚ£Ø2£©µÄĢõ¼žĻĀ£¬Čō³¬ŹŠ¼Ę»®ÓĆ²»³¬¹ż36000ŌŖ¹ŗ½ųČ”ÅÆĘ÷£¬ĒŅ¼×ÖÖČ”ÅÆĘ÷ÖĮÉŁ¹ŗ½ų10ĢØ£¬ ²¢½«Ėł»ńµĆµÄ×ī“óĄūČóČ«²æÓĆÓŚĪŖij¾“ĄĻŌŗ¹ŗĀņ1100ŌŖ/ĢصÄAŠĶ°“ĦĘ÷ŗĶ700ŌŖ/ĢصÄBŠĶ°“ĦĘ÷£® Ēó¹ŗĀņ°“ĦĘ÷µÄ·½°ø£®
”¾“š°ø”æ£Ø1£©¼×”¢ŅŅĮ½ÖÖČ”ÅÆĘ÷ĆæĢؽų¼Ū·Ö±šĪŖ2000ŌŖ”¢1500ŌŖ£»£Ø2£©y£½200x£«6000£»£Ø3£©ÓŠĮ½ÖÖ¹ŗĀņ·½°ø£ŗ¢ŁAŠĶ0ĢØ£¬BŠĶ12ĢØ£»¢ŚAŠĶ7ĢØ£¬BŠĶ1ĢØ£®
”¾½āĪö”æ
£Ø1£©øł¾ŻĢāŅāæÉŅŌĮŠ³öĻąÓ¦µÄ·½³Ģ£¬“Ó¶ųæÉŅŌ·Ö±šĒóµĆ¼×”¢ŅŅĮ½ÖÖČ”ÅÆĘ÷ĆæĢصĽų¼Ū£¬×¢Ņā·ÖŹ½·½³ĢŅŖ¼ģŃ飻
£Ø2£©øł¾ŻĢāŅāŗĶ£Ø1£©ÖŠµÄ“š°øæÉŅŌµĆµ½Ėł»ńĄūČóy£ØŌŖ£©Óė¼×ÖÖČ”ÅÆĘ÷x£ØĢØ£©Ö®¼äµÄŗÆŹż¹ŲĻµŹ½£»
£Ø3£©Éč¹ŗĀņ¼×ÖÖČ”ÅÆĘ÷nĢØ£¬øł¾ŻÉĢ³”¼Ę»®ÓĆ²»³¬¹ż36000ŌŖ¹ŗ½ųČ”ÅÆĘ÷¹²20ĢØ£¬æÉŅŌĒóµĆnµÄȔֵ·¶Ī§£¬“Ó¶ųæÉŅŌĒóµĆĖłÄÜ»ńµĆµÄ×ī“óĄūČó£¬Č»ŗóøł¾ŻĢāŅāĮŠ³ö¶žŌŖŅ»“Ī·½³Ģ£¬ÕŅµ½·ūŗĻĢāŅāµÄ½ā¼“æÉ£®
½ā£ŗ£Ø1£©ÉčŅŅÖÖČ”ÅÆĘ÷ĆæĢؽų¼ŪĪŖxŌŖ£¬Ōņ¼×ÖÖČ”ÅÆĘ÷ĆæĢؽų¼ŪĪŖ£Øx£«500£©ŌŖ£®
øł¾ŻĢāŅāµĆ£ŗ![]() £¬
£¬
½āµĆ£ŗx£½1500
¾¼ģŃéx£½1500ŹĒ·ÖŹ½·½³ĢµÄ½ā£¬ĒŅx£«500£½2000£¬
¼“¼×”¢ŅŅĮ½ÖÖČ”ÅÆĘ÷ĆæĢؽų¼Ū·Ö±šĪŖ2000ŌŖ”¢1500ŌŖ£»
£Ø2£©øł¾ŻĢāŅāµĆ£ŗy£½£Ø25002000£©x£«£Ø18001500£©£Ø20x£©£½200x£«6000£»
£Ø3£©Éč¹ŗĀņ¼×ÖÖČ”ÅÆĘ÷nĢØ£¬Ōņ¹ŗĀņŅŅÖÖČ”ÅÆĘ÷£Ø20n£©ĢØ£®
øł¾ŻĢāŅāµĆ£ŗ2000n£«1500£Ø20n£©”Ü36000£¬ĒŅn”Ż10£ØnĪŖÕżÕūŹż£©
½āµĆ£ŗ10”Ün”Ü12
µ±n£½12Ź±£¬×ī“óĄūČóĪŖ8400ŌŖ
Éč¹ŗĀņAŠĶ°“ĦĘ÷aĢØ£¬¹ŗĀņBŠĶ°“ĦĘ÷bĢØ£¬Ōņ1100a£«700b£½8400£¬
¹ŹÓŠĮ½ÖÖ¹ŗĀņ·½°ø£ŗ¢ŁAŠĶ0ĢØ£¬BŠĶ12ĢØ£»¢ŚAŠĶ7ĢØ£¬BŠĶ1ĢØ£®



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
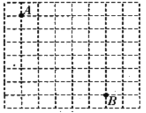
”¾ĢāÄæ”æČēĶ¼ĖłŹ¾µÄ·½øńÖ½ÖŠµÄĆæøöŠ”Õż·½ŠĪµÄ±ß³¤¾łĪŖ1£¬µćA”¢BŌŚŠ”Õż·½ŠĪµÄ¶„µćÉĻ.ŌŚĶ¼ÖŠ»³ö”÷ABC(µćCŌŚŠ”Õż·½ŠĪµÄ¶„µćÉĻ)£¬Ź¹”÷ABCĪŖÖ±½ĒČż½ĒŠĪ.
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
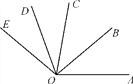
”¾ĢāÄæ”æČēĶ¼£¬OBĪŖ”ĻAOCµÄĘ½·ÖĻߣ¬ODŹĒ”ĻCOEµÄĘ½·ÖĻߣ®
(1)Čē¹ū”ĻAOB£½40”ć£¬”ĻDOE£½30”ć£¬ÄĒĆ“”ĻBODĪŖ¶ąÉŁ¶Č£æ
(2)Čē¹ū”ĻAOE£½140”ć£¬”ĻCOD£½30”ć£¬ÄĒĆ“”ĻAOBĪŖ¶ąÉŁ¶Č£æ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
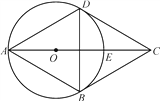
”¾ĢāÄæ”æŅŃÖŖ£ŗČēĶ¼£¬ĖıߊĪABCDĪŖĮāŠĪ£¬”÷ABDµÄĶā½ÓŌ²”ŃOÓėCDĻąĒŠÓŚµćD£¬½»ACÓŚµćE.
(1)ÅŠ¶Ļ”ŃOÓėBCµÄĪ»ÖĆ¹ŲĻµ£¬²¢ĖµĆ÷ĄķÓÉ£»
£Ø2£©ČōCE=2£¬Ēó”ŃOµÄ°ė¾¶r.
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æĮ½æéµČŃüÖ±½ĒČż½ĒŠĪÖ½Ę¬AOBŗĶCOD°“Ķ¼1ĖłŹ¾·ÅÖĆ£¬Ö±½Ē¶„µćÖŲŗĻŌŚµćO“¦£¬AB=25£¬CD=17£®±£³ÖÖ½Ę¬AOB²»¶Æ£¬½«Ö½Ę¬CODČʵćOÄꏱÕėŠż×Ŗ¦Į£Ø0”ć<¦Į<90”ć£©½Ē¶Č£¬ČēĶ¼2ĖłŹ¾£®
£Ø1£©ĄūÓĆĶ¼2Ö¤Ć÷AC=BDĒŅAC”ĶBD£»
£Ø2£©µ±BDÓėCDŌŚĶ¬Ņ»Ö±ĻßÉĻ£ØČēĶ¼3£©Ź±£¬ĒóACµÄ³¤ŗĶ¦ĮµÄÕżĻŅÖµ£®

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
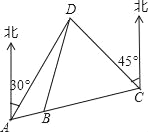
”¾ĢāÄæ”æ”°±¼ÅÜ°É£¬ŠÖµÜ£””±½ŚÄæ×éŌ¤Éč¼ĘŅ»øöŠĀÓĪĻ·£ŗ”°±¼ÅÜ”±Ā·ĻßA”¢B”¢C”¢DĖĵŲ£¬ČēĶ¼A”¢B”¢CČżµŲŌŚĶ¬Ņ»Ö±ĻßÉĻ£¬DŌŚA±±Ę«¶«30”ć·½Ļņ£¬ŌŚC±±Ę«Ī÷45”ć·½Ļņ£¬CŌŚA±±Ę«¶«75”ć·½Ļņ£¬ĒŅBD=BC=40m£¬“ÓAµŲµ½DµŲµÄ¾ąĄėŹĒ_____m£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
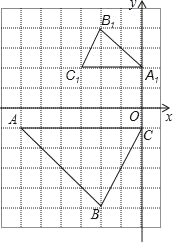
”¾ĢāÄæ”æČēĶ¼£¬”÷ABCÓė”÷A1B1C1ŹĒĪ»ĖĘĶ¼ŠĪ£®
£Ø1£©ŌŚĶųøńÉĻ½ØĮ¢Ę½ĆęÖ±½Ē×ų±źĻµ£¬Ź¹µĆµćAµÄ×ų±źĪŖ£Ø©6£¬©1£©£¬µćC1µÄ×ų±źĪŖ£Ø©3£¬2£©£¬ŌņµćBµÄ×ų±źĪŖ”” ””£»
£Ø2£©ŅŌµćAĪŖĪ»ĖĘÖŠŠÄ£¬ŌŚĶųøńĶ¼ÖŠ×÷”÷AB2C2£¬Ź¹”÷AB2C2ŗĶ”÷ABCĪ»ĖĘ£¬ĒŅĪ»ĖʱČĪŖ1£ŗ2£»
£Ø3£©ŌŚĶ¼ÉĻ±ź³ö”÷ABCÓė”÷A1B1C1µÄĪ»ĖĘÖŠŠÄP£¬²¢Š“³öµćPµÄ×ų±źĪŖ”” ””£¬¼ĘĖćĖıߊĪABCPµÄÖܳ¤ĪŖ”” ””£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
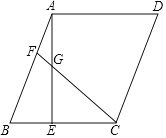
”¾ĢāÄæ”æŌŚABCDÖŠ£¬AE”ĶBCÓŚµćE£¬FĪŖAB±ßÉĻŅ»µć£¬Į¬½ÓCF£¬½»AEÓŚµćG£¬CF£½CB£½AE£®
£Ø1£©ČōAB![]() £¬BC
£¬BC![]() £¬ĒóCEµÄ³¤£»
£¬ĒóCEµÄ³¤£»
£Ø2£©ĒóÖ¤£ŗBE£½CG©AG£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŌĶĮ½āĢā¹ż³Ģ,»Ų“šĪŹĢā.
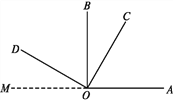
ČēĶ¼,OCŌŚ”ĻAOBÄŚ,”ĻAOBŗĶ”ĻCOD¶¼ŹĒÖ±½Ē,ĒŅ”ĻBOC=30”ć,Ēó”ĻAODµÄ¶ČŹż.
½ā:¹żOµć×÷ÉäĻßOM,Ź¹µćM,O,AŌŚĶ¬Ņ»Ö±ĻßÉĻ.
ŅņĪŖ”ĻMOD+”ĻBOD=90”ć,”ĻBOC+”ĻBOD=90”ć,ĖłŅŌ”ĻBOC=”ĻMOD,
ĖłŅŌ”ĻAOD=180”ć-”ĻBOC=180”ć-30”ć=150”ć.
(1)Čē¹ū”ĻBOC=60”ć,ÄĒĆ“”ĻAODµČÓŚ¶ąÉŁ¶Č?Čē¹ū”ĻBOC=n”ć,ÄĒĆ“”ĻAODµČÓŚ¶ąÉŁ¶Č?
(2)Čē¹ū”ĻAOB=”ĻDOC=x”ć,”ĻAOD=y”ć,Ēó”ĻBOCµÄ¶ČŹż.
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com