
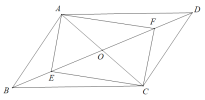
【题目】如图,平行四边形ABCD中,AC、BD相交于点O,E、F是对角线BD上的点,且BE=DF,连接AE、CE、CF、AF.
(1)求证:AE=CF;
(2)若平行四边形ABCD的面积是12,△OCF的面积是2,求△ADF的面积.
科目:初中数学 来源: 题型:
【题目】 若一个三角形一条边的平方等于另两条边的乘积,我们把这个三角形叫做比例三角形.
(1)已知△ABC是比例三角形,AB=2,BC=3,请直接写出所有满足AC条件的长;
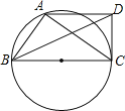
(2)如图,点A在以BC为直径的圆上,BD平分∠ABC,AD∥BC,∠ADC=90°.
①求证:△ABC为比例三角形;
②求![]() 的值.
的值.
(3)若以点C为顶点的抛物线y=mx2-4mx-12m(m<0)与x轴交于A、B两点,△ABC是比例三角形,若点M(x0,y0)为该抛物线上任意一点,总有n-![]() ≤-
≤-![]() my02-40
my02-40![]() y0+298成立,求实数n的最大值.
y0+298成立,求实数n的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,矩形OABC的顶点C在x轴的负半轴上,点A在y轴正半轴上,矩形OABC的面积为8![]() .把矩形OABC沿DE翻折,使点B与点O重合,点C落在第三象限的G点处,作EH⊥x轴于H,过E点的反比例函数y=
.把矩形OABC沿DE翻折,使点B与点O重合,点C落在第三象限的G点处,作EH⊥x轴于H,过E点的反比例函数y=![]() 图象恰好过DE的中点F.则k=_____,线段EH的长为:_____.
图象恰好过DE的中点F.则k=_____,线段EH的长为:_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,AD=6,E为AB的中点,将△ADE沿DE翻折得到△FDE,延长EF交BC于G,FH⊥BC,垂足为H,延长DF交BC与点M,连接BF、DG.以下结论:①∠BFD+∠ADE=180°;②△BFM为等腰三角形;③△FHB∽△EAD;④BE=2FM⑤S△BFG=2.6 ⑥sin∠EGB=![]() ;其中正确的个数是( )
;其中正确的个数是( )

A.3B.4C.5D.6
查看答案和解析>>
科目:初中数学 来源: 题型:
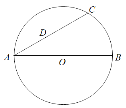
【题目】如图,线段AB是⊙O的直径,点C在⊙O上,且∠CAB=30°,设点D是线段AC上任意一点(不含端点),连接OD,当![]() CD+OD的最小值为9时,则⊙O的直径AB的长为_____.
CD+OD的最小值为9时,则⊙O的直径AB的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
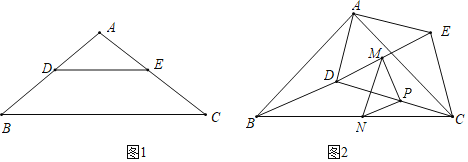
【题目】如图1,在![]() 中,点D、E分别在AB、AC上,
中,点D、E分别在AB、AC上,![]() ,
,![]() ,
,
![]() 求证:
求证:![]() ;
;
![]() 若
若![]() ,把
,把![]() 绕点A逆时针旋转到图2的位置,点M,P,N分别为DE,DC,BC的中点,连接MN,PM,PN.
绕点A逆时针旋转到图2的位置,点M,P,N分别为DE,DC,BC的中点,连接MN,PM,PN.
![]() 判断
判断![]() 的形状,并说明理由;
的形状,并说明理由;
![]() 把
把![]() 绕点A在平面内自由旋转,若
绕点A在平面内自由旋转,若![]() ,
,![]() ,试问
,试问![]() 面积是否存在最大值;若存在,求出其最大值
面积是否存在最大值;若存在,求出其最大值![]() 若不存在,请说明理由.
若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小林在没有量角器和圆规的情况下,利用刻度尺和一副三角板画出了一个角的平分线,他的做法是这样的:如图,
①利用刻度尺在∠AOB的两边OA,OB上分别取OM=ON;
②利用两个三角板,分别过点M,N画OM,ON的垂线,交点为P;
③画射线OP.则射线OP为∠AOB的平分线.

(1)请写出射线OP为∠AOB的平分线的证明过程.
(2)请根据你的证明过程,写出小林的画法的依据______.
查看答案和解析>>
科目:初中数学 来源: 题型:
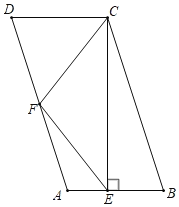
【题目】如图,在四边形ABCD中,AD∥BC,AD=BC=2AB,F是AD的中点,作CE⊥AB,垂足E在线段AB上,连接EF、CF.
(1)若∠ADC=80°,求∠ECF;
(2)求证:∠ECF=∠CEF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了丰富校园文化,某学校决定举行学生趣味运动会,将比赛项目确定为袋鼠跳、夹球跑、跳大绳、绑腿跑和拔河赛五种.为了解学生对这五项运动的喜欢情况,随机调查了该校a名学生最喜欢的一种项目(每名学生必选且只能选择五项中的一种)并将调查结果绘制成如下不完整的统计图表:
学生最喜欢的活动项目的人数统计表 | ||
项目 | 学生数(名) | 百分比(%) |
袋鼠跳 | 45 | 15 |
夹球跑 | 30 | c |
跳大绳 | 75 | 25 |
绑腿跑 | b | m |
拔河赛 | 90 | 30 |

根据图表中提供的信息,解答下列问题:
(1)a= ,b= ,c= ;
(2)请将条形统计图补充完整;
(3)根据调查结果,请你估计该校3000名学生中有多少名学生最喜欢绑腿跑.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com