

分析 (1)作高AF,先求△ABD的面积,再求出高线AF的长,根据三角函数求x+y的度数;
(2)作辅助线,利用同样的方法求出sin(α-β)的值.
解答 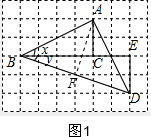 解:(1)如图1,过A作AF⊥BD于F,
解:(1)如图1,过A作AF⊥BD于F,
S△ABD=4×6-$\frac{1}{2}$×2×4-$\frac{1}{2}$×2×4-$\frac{1}{2}$×2×6=10,
由勾股定理得:BD=$\sqrt{{2}^{2}+{6}^{2}}$=2$\sqrt{10}$,
AB=$\sqrt{{2}^{2}+{4}^{2}}$=2$\sqrt{5}$,
∴S△ABD=$\frac{1}{2}$BD•AF=10,
$\frac{1}{2}$×2$\sqrt{10}$×AF=10,
AF=$\sqrt{10}$,
在Rt△ABF中,sin(x+y)=$\frac{AF}{AB}$=$\frac{\sqrt{10}}{2\sqrt{5}}$=$\frac{\sqrt{2}}{2}$,
∵sin45°=$\frac{\sqrt{2}}{2}$,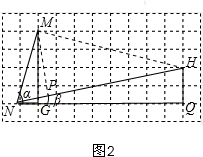
∴x+y=45°,
故答案为:45;
(2)如图2,∠MNH=α-β,
连接MH,过M作MP⊥NH于P,
S△MNH=4×9-$\frac{1}{2}$×1×4-$\frac{1}{2}$×2×9-$\frac{1}{2}$×2×8=17,
由勾股定理得:NH=$\sqrt{{2}^{2}+{9}^{2}}$=$\sqrt{85}$,
MN=$\sqrt{{1}^{2}+{4}^{2}}$=$\sqrt{17}$,
∴S△MNH=$\frac{1}{2}$NH•MP=17,
$\frac{1}{2}$×$\sqrt{85}$×MP=17,
MP=$\frac{2\sqrt{85}}{5}$,
在Rt△MNP中,sin(α-β)=$\frac{MP}{MN}$=$\frac{\frac{2\sqrt{85}}{5}}{\sqrt{17}}$=$\frac{2\sqrt{5}}{5}$,
故答案为:$\frac{2\sqrt{5}}{5}$.
点评 本题考查了应用与设计作图,还考查了解直角三角形;首先要熟记特殊的三角函数值和三个三角函数的定义,利用面积法先求面积再求高,与勾股定理相结合,求边的长度;从而得出各个三角函数值.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
 如图所示,某公司入口处原有三级台阶,每级台阶高为20cm,台阶面的宽为30cm,为了方便残疾人士,拟将台阶改为坡角为12°的斜坡,设原台阶的起点为A,斜坡的起点为C,求AC的长度(精确到1cm)
如图所示,某公司入口处原有三级台阶,每级台阶高为20cm,台阶面的宽为30cm,为了方便残疾人士,拟将台阶改为坡角为12°的斜坡,设原台阶的起点为A,斜坡的起点为C,求AC的长度(精确到1cm)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
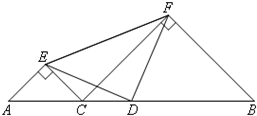 已知:如图,D为线段AB的中点,在AB上任取一点C(不与点A,B,D重合),分别以AC,BC为斜边在AB同侧作等腰Rt△ACE与等腰Rt△BCF,∠AEC=∠CFB=90°,连接DE,DF,EF.
已知:如图,D为线段AB的中点,在AB上任取一点C(不与点A,B,D重合),分别以AC,BC为斜边在AB同侧作等腰Rt△ACE与等腰Rt△BCF,∠AEC=∠CFB=90°,连接DE,DF,EF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,一块大的三角板ABC,D是AB上一点,现要求过点D割出一块小的三角板ADE,使∠ADE=∠ABC,
如图,一块大的三角板ABC,D是AB上一点,现要求过点D割出一块小的三角板ADE,使∠ADE=∠ABC,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com