
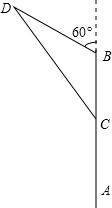
 如图,海面上离船A的正北方向100海里处有一船B正以每小时20海里的速度沿北偏西60°的方向行驶,而船A以每小时15海里的速度向正北方向行驶.若两船同时出发,则几小时后两船最近.
如图,海面上离船A的正北方向100海里处有一船B正以每小时20海里的速度沿北偏西60°的方向行驶,而船A以每小时15海里的速度向正北方向行驶.若两船同时出发,则几小时后两船最近. 分析 根据已知构造直角三角形,进而表示出各边长再利用勾股定理求出答案.
解答 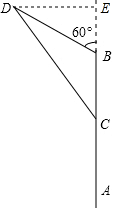 解:过点D作DE⊥AB于点E,
解:过点D作DE⊥AB于点E,
设x小时后,B船至D处,A船至C处.则BD=20x,BC=100-15x>0(0<x<$\frac{20}{3}$),可得:BE=10x,
故EC=100-15x+10x=100-5x,DE=10$\sqrt{3}x$,
则DC2=DE2+CE2=(10$\sqrt{3}$x)2+(100-5x)2
=300x2+10000+25x2-1000x
=325x2-1000x+10000
=325(x-$\frac{20}{13}$)2+10000-$\frac{10000}{13}$
=325(x-$\frac{20}{13}$)2+$\frac{120000}{13}$,(0<x<$\frac{20}{3}$),
故x=$\frac{20}{13}$小时后,两船最近,
点评 此题主要考查了勾股定理的应用以及二次函数最值求法,正确表示出各边长是解题关键.


 一课一练课时达标系列答案
一课一练课时达标系列答案科目:初中数学 来源: 题型:解答题
 如图,有一个边长为4cm的正方形和一个长为8cm、宽为4cm的长方形拼接成一个大长方形,现制作一个与大长方形面积相等的正方形,则这个大正方形的边长是多少?(结果保留小数点后两位)
如图,有一个边长为4cm的正方形和一个长为8cm、宽为4cm的长方形拼接成一个大长方形,现制作一个与大长方形面积相等的正方形,则这个大正方形的边长是多少?(结果保留小数点后两位)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
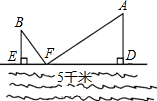 如图,大江的同一侧有A,B两个工厂,它们都有垂直于江边的小路AD,BE,AD=3千米,BE=2千米,且两条小路之间的距离为5千米.现要在江边建一个供水站F向A,B两厂送水,若供水管路最短,则EF=2千米.
如图,大江的同一侧有A,B两个工厂,它们都有垂直于江边的小路AD,BE,AD=3千米,BE=2千米,且两条小路之间的距离为5千米.现要在江边建一个供水站F向A,B两厂送水,若供水管路最短,则EF=2千米.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
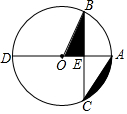 如图,在☉O中,直径AD交弦BC于E,OE=AE,∠ACB=30°,BC=4,则图中阴影部分的面积为( )
如图,在☉O中,直径AD交弦BC于E,OE=AE,∠ACB=30°,BC=4,则图中阴影部分的面积为( )| A. | $\frac{8}{9}π-\frac{{2\sqrt{3}}}{3}$ | B. | $\frac{8}{9}π-\frac{{4\sqrt{3}}}{3}$ | C. | $\frac{{4\sqrt{3}}}{18}π-\frac{{2\sqrt{3}}}{3}$ | D. | $\frac{16}{9}π-\frac{{2\sqrt{3}}}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com