
【题目】数轴上任意两点之间的距离均可用“右﹣左”表示,即右边的数(较大)减去左边的数(较小).已知数轴上两点A、B对应的数分别为﹣2、5,则A、B两点之间的距离记为AB,且AB=5﹣(﹣2)=7.P为数轴上的动点,其对应的数为x.
![]()
(1)若点P到A,B两点的距离相等,写出点P对应的数;
(2)数轴上是否存在点P,使点P到A,B两点的距离之和为11,若存在,请求出x的值;若不存在,请说明理由;
(3)若点P在原点,现在A,B,P三个点均向左匀速运动,其中点P的速度为每秒1个单位;A,B两点中有一个点速度与点P的速度一致,另一个点以每秒3单位的速度运动;则几秒后点P到A,B两点的距离相等?
【答案】(1)点P对应的数为1.5;(2)x=7或﹣4;(3)①当点A与点P的运动速度相等时,![]() 秒或
秒或![]() 秒后点P到A,B两点的距离相等;②当点B与点P的运动速度相等时,
秒后点P到A,B两点的距离相等;②当点B与点P的运动速度相等时,![]() 秒后点P到A,B两点的距离相等.
秒后点P到A,B两点的距离相等.
【解析】
(1)根据P点表示的数为x,利用距离相等列出方程解答即可;
(2)分当P在AB之间(包括与A,B重合)时,当P点在A点的左边时,当P点在B点的右边时,根据P点到A,B两点的距离和为11列出方程解答即可;
(3)设出运动时间,分情况讨论:①当点A与点P的运动速度相等时;②当点B与点P的运动速度相等时,分别根据两点之间的距离求法表示出PA和PB,结合PA=PB列出方程求解即可.
解:(1)由题意得x﹣(﹣2)=5﹣x,
解得x=1.5,
即点P对应的数为1.5;
(2)①当P在AB之间(包括与A,B重合)时,
PA+PB=x﹣(﹣2)+5﹣x=7,不符合要求,
②当P在B的右边时,PA+PB=x﹣(﹣2)+x﹣5=2x﹣3,
令2x﹣3=11,
解得x=7,
③当P在A的左边时,PA+PB=﹣2﹣x+5﹣x=3﹣2x,
令3﹣2x=11,
解得x=﹣4,
综上所述,x=7或﹣4;
(3)设运动时间为t秒,
由题意可知:A、B对应的数分别为﹣2、5,P对应的数为0,
①当点A与点P的运动速度相等时,t秒后A点表示的数为-2-t,P点表示的数为-t,B点表示的数为5-3t,
则PA=-t-(-2-t)=2,PB=![]() ,
,
由点P到A,B两点的距离相等得:![]() ,
,
解得:t=![]() 或
或![]() ;
;
②当点B与点P的运动速度相等时,t秒后A点表示的数为-2-3t,P点表示的数为-t,B点表示的数为5-t,
则PA=-t-(-2-3t)=2+2t,PB=5-t-(-t)=5,
由点P到A,B两点的距离相等得:5=2+2t,
解得t=![]() ,
,
综上所述:当点A与点P的运动速度相等时,![]() 秒或
秒或![]() 秒后点P到A,B两点的距离相等;当点B与点P的运动速度相等时,
秒后点P到A,B两点的距离相等;当点B与点P的运动速度相等时,![]() 秒后点P到A,B两点的距离相等.
秒后点P到A,B两点的距离相等.


 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,AE⊥BC,垂足为点E,CE=CD,点F为CE的中点,点G为CD上的一点,连接DF,EG,AG,∠1=∠2.

(1)若CF=2,AE=3,求BE的长;
(2)求证:∠CEG=![]() ∠AGE.
∠AGE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市绿化部门决定利用现有的不同种类花卉搭配园艺造型,摆放于城区主要大道的两侧.A、B两种园艺造型均需用到杜鹃花,A种造型每个需用杜鹃花25盆,B种造型每个需用杜鹃花35盆,解答下列问题:
(1)已知人民大道两侧搭配的A、B两种园艺造型共60个,恰好用了1700盆杜鹃花,A、B两种园艺造型各搭配了多少个?
(2)如果搭配一个A种造型的成本W与造型个数![]() 的关系式为:W=100―
的关系式为:W=100―![]() x (0<x<50),搭配一个B种造型的成本为80元.现在观海大道两侧也需搭配A、B两种园艺造型共50个,要求每种园艺造型不得少于20个,并且成本总额y(元)控制在4500元以内. 以上要求能否同时满足?请你通过计算说明理由.
x (0<x<50),搭配一个B种造型的成本为80元.现在观海大道两侧也需搭配A、B两种园艺造型共50个,要求每种园艺造型不得少于20个,并且成本总额y(元)控制在4500元以内. 以上要求能否同时满足?请你通过计算说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:在数轴上![]() 点表示数
点表示数![]() ,
,![]() 点表示数6,
点表示数6,
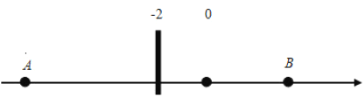
(1)A、B两点之间的距离等于_________;
(2)在数轴上有一个动点![]() ,它表示的数是
,它表示的数是![]() ,则
,则![]() 的最小值是_________;
的最小值是_________;
(3)若点![]() 与点
与点![]() 之间的距离表示为
之间的距离表示为![]() ,点
,点![]() 与点
与点![]() 之间的距离表示为
之间的距离表示为![]() ,请在数轴上找一点
,请在数轴上找一点![]() ,使
,使![]() ,则
,则![]() 点表示的数是_________;
点表示的数是_________;
(4)若在原点![]() 的左边2个单位处放一挡板,一小球甲从点
的左边2个单位处放一挡板,一小球甲从点![]() 处以5个单位/秒的速度向右运动;同时另一小球乙从点
处以5个单位/秒的速度向右运动;同时另一小球乙从点![]() 处以2个单位/秒的速度向左运动,在碰到挡板后(忽略球的大小,可看作一点)两球分别以原来的速度向相反的方向运动,设运动时间为
处以2个单位/秒的速度向左运动,在碰到挡板后(忽略球的大小,可看作一点)两球分别以原来的速度向相反的方向运动,设运动时间为![]() 秒,请用
秒,请用![]() 来表示甲、乙两小球之间的距离
来表示甲、乙两小球之间的距离![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,OD平分∠BOC,OE平分∠AOC.
(1)若∠BOC=60°,∠AOC=40°,求∠DOE的度数;
(2)若∠DOE=n°,求∠AOB的度数;
(3)若∠DOE+∠AOB=180°,求∠AOB与∠DOE的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下面的推理过程.
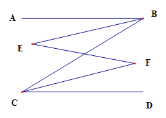
如图,AB∥CD,BE、CF分别是∠ABC和∠BCD的平分线.求证:∠E=∠F
证明:∵AB∥CD(已知)
∴∠ABC=∠BCD( )
∵BE、CF分别是∠ABC和∠BCD的平分线(已知)
∴∠CBE=![]() ∠ABC,∠BCF=
∠ABC,∠BCF=![]() ∠BCD( )
∠BCD( )
∴∠CBE=∠BCF( )
∴BE∥CF( )
∴∠E=∠F( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,E是正方形ABCD外一点,且DE=CE=![]() ,连接AE.
,连接AE.
(1)将△ADE绕点D逆时针旋转90°,作出旋转后的图形.
(2)如果∠AED=15°,判断△DEC的形状,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某星期六上午,小明从家出发跑步去公园,在公园停留了一会儿打车回家.图中折线表 示小明离开家的路程y(米)和所用时间x(分)之间的函数关系,则下列说法中错误的是( )
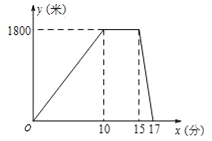
A.小明在公园休息了5分钟
B.小明乘出租车用了17分
C.小明跑步的速度为180米/分
D.出租车的平均速度是900米/分
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com