
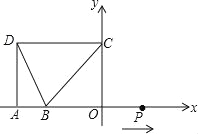
【题目】如图,在坐标系xOy中,已知D(﹣5,4),B(﹣3,0),过D点分别作DA、DC垂直于x轴,y轴,垂足分别为A、C两点,动点P从O点出发,沿x轴以每秒1个单位长度的速度向右运动,运动时间为t秒.
(1)当t为何值时,PC∥DB;
(2)当t为何值时,PC⊥BC;
(3)以点P为圆心,PO的长为半径的⊙P随点P的运动而变化,当⊙P与△BCD的边(或边所在的直线)相切时,求t的值.
【答案】(1)2(2)![]() (3)4,12,t=(6
(3)4,12,t=(6![]() +12)
+12)
【解析】
试题分析:(1)过D点分别作DA、DC垂直于x轴,y轴,垂足分别为A、C两点,求出DC=5,OC=4,OB=3,根据四边形DBPC是平行四边形求出DC=BP=5,求出OP=2即可;
(2)证△PCO∽△CBO,得出![]() ,求出OP=
,求出OP=![]() 即可;
即可;
(3)设⊙P的半径是R,分为三种情况:①当⊙P与直线DC相切时,过P作PM⊥DC交DC延长线于M,求出PM、OP的长即可;
②当⊙P与BC相切时,根据△COB∽△PBM得出![]() ,求出R=12即可;③当⊙P与DB相切时,证△ADB∽△MPB得出
,求出R=12即可;③当⊙P与DB相切时,证△ADB∽△MPB得出![]() ,求出R即可.
,求出R即可.
试题解析:(1)∵D(﹣5,4),B(﹣3,0),过D点分别作DA、DC垂直于x轴,y轴,垂足分别为A、C两点,
∴DC=5,OC=4,OB=3,
∵DC⊥y轴,x轴⊥y轴,
∴DC∥BP,
∵PC∥DB,
∴四边形DBPC是平行四边形,
∴DC=BP=5,
∴OP=5﹣3=2,
2÷1=2,
即当t为2秒时,PC∥BD;
(2)∵PC⊥BC,x轴⊥y轴,
∴∠COP=∠COB=∠BCP=90∴,
∴∠PCO+∠BCO=90°,∠CPO+∠PCO=90°,
∴∠CPO=∠BCO,
∴△PCO∽△CBO,
∴![]() ,
,
∴![]() ,
,
∴OP=![]() ,
,
![]() ÷1=
÷1=![]() ,
,
即当t为![]() 秒时,PC⊥BC;
秒时,PC⊥BC;
(3)设⊙P的半径是R,
分为三种情况:①当⊙P与直线DC相切时,
如图1,过P作PM⊥DC交DC延长线于M,
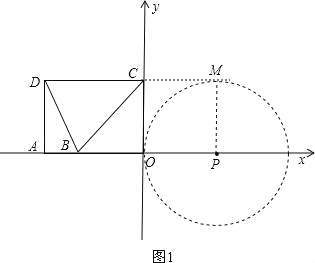
则PM=OC=4=OP,
4÷1=4,
即t=4;
②如图2,当⊙P与BC相切时,
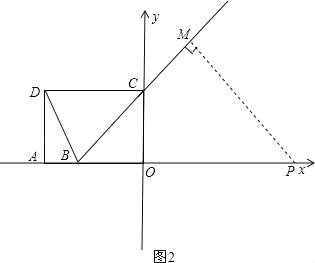
∵∠BOC=90°,BO=3,OC=4,由勾股定理得:BC=5,
∵∠PMB=∠COB=90°,∠CBO=∠PBM,
∴△COB∽△PMB,
∴![]() ,
,
∴![]() ,
,
R=12,
12÷1=12,
即t=12秒;
③根据勾股定理得:BD=![]() =2
=2![]() ,
,
如图3,当⊙P与DB相切时,
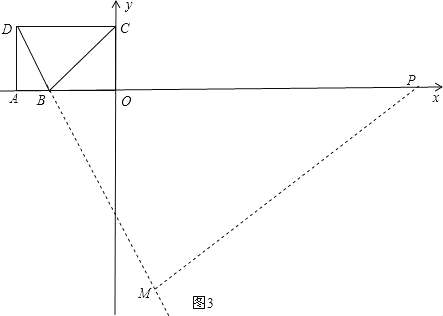
∵∠PMB=∠DAB=90°,∠ABD=∠PBM,
∴△ADB∽△MPB,
∴![]() ,
,
∴![]() ,
,
R=6![]() +12;
+12;
(6![]() +12)÷1=6
+12)÷1=6![]() +12,
+12,
即t=(6![]() +12)秒.
+12)秒.


科目:初中数学 来源: 题型:
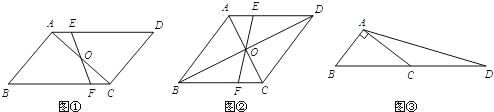
【题目】猜想:如图①,在ABCD中,点O是对角线AC的中点,过点O的直线分别交AD、BC于点E、F.若ABCD的面积是10,则四边形CDEF的面积是 .
探究:如图②,在菱形ABCD中,对角线AC、BD相交于点O,过点O的直线分别交AD、BC于点E、F.若AC=4,BD=8,求四边形ABFE的面积.
应用:如图③,在Rt△ABC中,∠BAC=90°,延长BC到点D,使DC=BC,连结AD.若AC=4,![]() ,则△ABD的面积是 .
,则△ABD的面积是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列调查:
①机场对乘客进行安检; ②对北京世园会游客满意度的调查;
③对全省中学生视力情况的调查;④九年级一班要选出1人参加学校的100米比赛.
其中适合全面调查的是( )
A.②③B.①④C.②④D.①③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平直角坐标系中,如果抛物线y=4x2不动,而把x轴、y轴分别向上、向右平移2个单位,那么在新坐标系下抛物线的解析式是( )
A.y=4(x﹣2)2+2B.y=4(x+2)2﹣2
C.y=4(x﹣2)2﹣2D.y=4(x+2)2+2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2014年,长沙地铁2号线的开通运营,极大地缓解了城市中心的交通压力,为我市再次获评“中国最具幸福感城市”提供了有力支撑,据统计,长沙地铁2号线每天承动力约为185000人次,则数据185000用科学记数法表示为( )
A.1.85×105
B.1.85×104
C.1.8×105
D.18.5×104
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2020年是具有里程碑意义的一年,我们将全面建成小康社会,全面建设小康社会的基本标准包括:人均国内生产总值超过3000美元、城镇居民人均可支配收入1.8万元等十个方面.数据“1.8万元”用科学技术法表示为( ).
A.1.8×103元B.1.8×104元C.0.18×105元D.18000元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列去括号中,正确的是( )
A.a﹣(b﹣c)=a﹣b﹣c
B.c+2(a﹣b)=c+2a﹣b
C.a﹣(b﹣c)=a+b﹣c
D.a﹣(b﹣c)=a﹣b+c
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com