
美丽的东昌湖赋予江北水城以灵性,周边景点密布,如下图所示,A、B为湖滨的两个景点,C为湖北一个景点,景点B在景点C的正东,从景点A看,景点B在北偏东75°方向,景点C往北偏东30°方向。一游客自景点A驾船以每分钟20米的速度行驶了10分钟到达景点C,之后又以同样的速度驶向景点B,该游客从景点C到景点B需用多长时间(精确到1分钟)。(供选择数据:sin75°≈0.966,cos75°≈0.259,tan75°≈3.732,cot75°≈0.268,![]() ≈1.732)
≈1.732)
 t
t
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案科目:初中数学 来源: 题型:
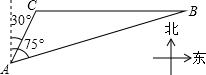 到1分钟)
到1分钟)查看答案和解析>>
科目:初中数学 来源:第1章《直角三角形的边角关系》中考题集(28):1.4 船有触角的危险吗(解析版) 题型:解答题

查看答案和解析>>
科目:初中数学 来源:第7章《锐角三角函数》中考题集(46):7.6 锐角三角函数的简单应用(解析版) 题型:解答题

查看答案和解析>>
科目:初中数学 来源:第28章《锐角三角函数》中考题集(45):28.2 解直角三角形(解析版) 题型:解答题

查看答案和解析>>
科目:初中数学 来源:第4章《锐角三角形》中考题集(39):4.3 解直角三角形及其应用(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com