
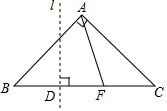
 如图,等腰Rt△ABC中,AB=AC=1,点F是边BC上不与点B、C重合的一个动点,直线l垂直平分BF,垂足为D,当△AFC是等腰三角形时,BD的长为$\frac{\sqrt{2}}{4}$或$\frac{\sqrt{2}-1}{2}$.
如图,等腰Rt△ABC中,AB=AC=1,点F是边BC上不与点B、C重合的一个动点,直线l垂直平分BF,垂足为D,当△AFC是等腰三角形时,BD的长为$\frac{\sqrt{2}}{4}$或$\frac{\sqrt{2}-1}{2}$. 分析 由勾股定理求出BC,分两种情况:①当AF=CF时,∠FAC=∠C=45°,∠AFC=90°,由等腰直角三角形的性质得出BF=CF=$\frac{1}{2}$BC=$\frac{\sqrt{2}}{2}$,得出BD=$\frac{1}{2}$BF=$\frac{\sqrt{2}}{4}$即可;
②当CF=CA=1时,BF=BC-CF=$\sqrt{2}$-1,得出BD=$\frac{1}{2}$BF=$\frac{\sqrt{2}-1}{2}$即可.
解答 解:∵等腰Rt△ABC中,AB=AC=1,
∴BC=$\sqrt{A{B}^{2}+A{C}^{2}}$=$\sqrt{2}$,
分两种情况:
①当AF=CF时,∠FAC=∠C=45°,
∴∠AFC=90°,
∴AF⊥BC,
∴BF=CF=$\frac{1}{2}$BC=$\frac{\sqrt{2}}{2}$,
∵直线l垂直平分BF,
∴BD=$\frac{1}{2}$BF=$\frac{\sqrt{2}}{4}$;
②当CF=CA=1时,BF=BC-CF=$\sqrt{2}$-1,
∵直线l垂直平分BF,
∴BD=$\frac{1}{2}$BF=$\frac{\sqrt{2}-1}{2}$;
故答案为:$\frac{\sqrt{2}}{4}$或$\frac{\sqrt{2}-1}{2}$.
点评 本题考查了等腰直角三角形的性质、勾股定理、线段垂直平分线的性质;熟练掌握等腰直角三角形的性质是解决问题的关键,注意分类讨论.


 习题精选系列答案
习题精选系列答案科目:初中数学 来源: 题型:填空题
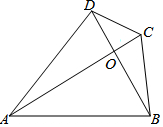 如图,在Rt△ABO中,∠AOB=90°,AO+BO=5,延长AO到C,使OC=3,延长BO到D,使OD=4,连接BC、CD、DA,则四边形ABCD面积的最大值为18.
如图,在Rt△ABO中,∠AOB=90°,AO+BO=5,延长AO到C,使OC=3,延长BO到D,使OD=4,连接BC、CD、DA,则四边形ABCD面积的最大值为18.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
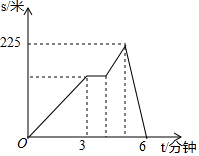 小明和小龙沿着一条笔直的马路进行长跑比赛,小明在比赛过程中始终领先小龙,并匀速跑完了全程,小龙匀速跑了几分钟后提速和小明保持速度一致,又过了1分钟,小龙因为体力问题,不得已又减速,并一直以这一速度完成了余下的比赛,完成比赛所用时间比小明多了1分钟,已知小明起跑后4分20秒时领先小龙175米,小明与小龙之间的距离s(单位:米)与他们所用时间t(单位:分钟)之间的函数关系如图所示.
小明和小龙沿着一条笔直的马路进行长跑比赛,小明在比赛过程中始终领先小龙,并匀速跑完了全程,小龙匀速跑了几分钟后提速和小明保持速度一致,又过了1分钟,小龙因为体力问题,不得已又减速,并一直以这一速度完成了余下的比赛,完成比赛所用时间比小明多了1分钟,已知小明起跑后4分20秒时领先小龙175米,小明与小龙之间的距离s(单位:米)与他们所用时间t(单位:分钟)之间的函数关系如图所示.| A. | ①②③ | B. | ②③④ | C. | ①②④ | D. | ①③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2$\sqrt{5}$ | B. | 2$\sqrt{5}$或5 | C. | 2$\sqrt{6}$ | D. | 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
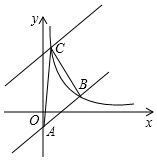 如图,在平面直角坐标系xOy中,直线y=x-2与y轴相交于点A,与反比例函数在第一象限内的图象相交于点B(m,2)
如图,在平面直角坐标系xOy中,直线y=x-2与y轴相交于点A,与反比例函数在第一象限内的图象相交于点B(m,2)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com