
【题目】如图①,在矩形![]() 中,动点
中,动点![]() 从点
从点![]() 出发,以2cm/s的速度沿
出发,以2cm/s的速度沿![]() 向终点
向终点![]() 移动,设移动时间为t(s).连接
移动,设移动时间为t(s).连接![]() ,以
,以![]() 为一边作正方形
为一边作正方形![]() ,连接
,连接![]() 、
、![]() .设
.设![]() 的面积为
的面积为![]() (cm2).
(cm2). ![]() 与t之间的函数关系如图②所示.
与t之间的函数关系如图②所示.
(1) ![]() cm,
cm,![]() cm;
cm;
(2) 点![]() 从点
从点![]() 到点
到点![]() 的移动过程中,点
的移动过程中,点![]() 的路径是_________________ cm.
的路径是_________________ cm.
(3)当![]() 为何值时,
为何值时,![]() 的面积最小?并求出这个最小值;
的面积最小?并求出这个最小值;
(4) 当![]() 为何值时,
为何值时,![]() 为等腰三角形?请直接写出结果。
为等腰三角形?请直接写出结果。
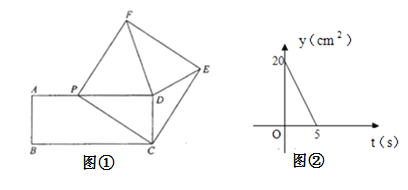
【答案】(1)4,10; (2)10; (3)当t=4时,最小值为6;(4)t=1,3,4 .
【解析】
(1)根据图②三角形PCD的面积,可得矩形的长和宽;
(2)由题意得:AP=t,PD=5-t,根据三角形面积公式可得y与t的关系式,由图②得:S△DEF+S△PDC=![]() S正方形EFPC,代入可得结论;
S正方形EFPC,代入可得结论;
(3)当△DEF为等腰三角形时,分三种情况进行讨论,根据全等三角形的性质计算PD和AP的长,可得t的值.
(1)由图②知:AD=5,
当t=0时,P与A重合,y=![]() ×AD×CD=5,
×AD×CD=5,
![]() ×5×CD=5,
×5×CD=5,
CD=2cm,
∵四边形ABCD是矩形,
∴AB=CD=2cm,
故答案为:2,5;
(2)由题意得:AP=t,PD=5-t,
∴y=![]() CDPD=
CDPD=![]() 2(5t)=5-t,
2(5t)=5-t,
∵四边形EFPC是正方形,
∴S△DEF+S△PDC=![]() S正方形EFPC,
S正方形EFPC,
∵PC2=PD2+CD2,
∴PC2=22+(5-t)2=t2-10t+29,
∴S△DEF=![]() (t2-10t+29)-(5-t)=
(t2-10t+29)-(5-t)=![]() t2-4t+
t2-4t+![]() =
=![]() (t-4)2+
(t-4)2+![]() ,
,
当t为4时,△DEF的面积最小,且最小值为![]() ;
;
(3)当△DEF为等腰三角形时,分三种情况:
①当FD=FE时,如下图所示,过F作FG⊥AD于G,
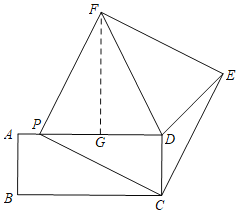
∵四边形EFPC是正方形,
∴PF=EF=PC,∠FPC=90°,
∴PF=FD,
∵FG⊥PD,
∴PG=DG=![]() PD,
PD,
∵∠FPG+∠CPD=∠CPD+∠DCP=90°,
∴∠FPG=∠DCP,
∵∠FGP=∠PDC=90°,
∴△FPG≌△PDC(AAS),
∴PG=DC=2,
∴PD=4,
∴AP=5-4=1,
即t=1;
②当DE=D时,如下图所示,E在AD的延长线上,此时正方形EFPC是正方形,PD=CD=2
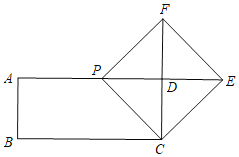
∴AP=t=5-2=3
③当DE=EF时,如下图所示,过E作EG⊥CD于G,
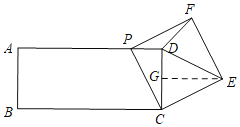
∵FE=DE=EC,
∴CG=DG=![]() CD=1,
CD=1,
同理得:△PDC≌△CGE(AAS),
∴PD=CG=1,
∴AP=t=5-1=4,
综上,当t=1s或3s或4s时,△DEF为等腰三角形.


科目:初中数学 来源: 题型:
【题目】已知某景区门票价格为80元/人,景区为吸引游客,对门票价格进行动态管理,非节假日打a折(如打2折,即是按原价的20%出售),节假日期间,10人以下(包括10人)不打折,10人以上超过10人的部分打b折,设游客为x人,门票费用为y元,非节假日门票费用y1(元)及节假日门票费用y2(元)与游客x(人)之间的函数关系如图所示.
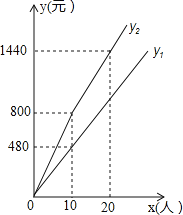
(1)a= ,b= ;
(2)直接写出y1、y2与x之间的函数关系式;
(3)一公司准备安排公司50名职工在“五一”假期时到此景区春游,而公司接到任务有一部分职工在“五一”当天需要加班,只能安排他们延期(非节假日)游玩,公司根据安排,春游期间除去其他费用,能提供的门票费用不超过3040元,那么公司至少安排多少人提前(五一期间)春游?
查看答案和解析>>
科目:初中数学 来源: 题型:
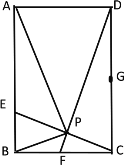
【题目】如图,矩形ABCD 中,AD=4cm,AB=6cm,动点 E从 B向A运动,速度为每秒2cm;同时,动点F从 C向B运动,速度为每秒3cm;任意一点到达终点后,两点都停止运动。连接CE、DF交于点P,连接BP,
(1)求证:△EBC ∽ △FCD
(2)BP最小值是多少?此时点F运动了多少秒?
(3)在该运动过程中, tan∠PAD的最大值是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,BD为一条对角线,AD∥BC,AD=2BC,∠ABD=90°,E为AD的中点,连接BE.
(1)求证:四边形BCDE为菱形;
(2)连接AC,若AC平分∠BAD,BC=1,求AC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲口袋中有1个红球、1个白球,乙口袋中有1个红球、2个白球,这些球除颜色外无其他差别.
(1)从甲口袋中随机摸出1个球,恰好摸到红球的概率为 ;
(2)分别从甲、乙两个口袋中各随机摸出1个球,请用列表或画树状图的方法求摸出的2个球都是白球的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
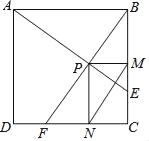
【题目】如图,在边长为2的正方形BCD中,动点F、E分别以相同的速度从D、C两点同时出发向C和B运动(任何一个点到达即停止),过点P作PM∥CD交BC于M点,PN∥BC交CD于N点,连接MN,在运动过程中,下列结论:①△ABE≌△BCF;②AE⊥BF;③CF2=PEBF;④线段MN的最小值为![]() ﹣1.其中正确的结论有_____.
﹣1.其中正确的结论有_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某厂家以A、B两种原料,利用不同的工艺手法生产出了甲、乙两种袋装产品,其中,甲产品每袋含1.5千克A原料、1.5千克B原料;乙产品每袋含2千克A原料、1千克B原料.甲、乙两种产品每袋的成本价分别为袋中两种原料的成本价之和.若甲产品每袋售价72元,则利润率为20%.某节庆日,厂家准备生产若干袋甲产品和乙产品,甲产品和乙产品的数量和不超过100袋,会计在核算成本的时候把A原料和B原料的单价看反了,后面发现如果不看反,那么实际成本比核算时的成本少500元,那么厂家在生产甲乙两种产品时实际成本最多为_____元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD是△ABC的边BC的中线,E是AD的中点,过点A作AF∥BC,交BE的延长线于点F,连接CF,BF交AC于G.
(1)若四边形ADCF是菱形,试证明△ABC是直角三角形;
(2)求证:CG=2AG.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=﹣x2+2x+8与x轴交于B、C两点,点D平分BC.若在x轴上侧的A点为抛物线上的动点,且∠BAC为锐角,则AD的取值范围是_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com