
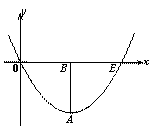
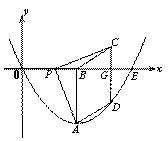
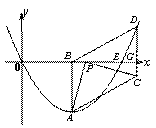
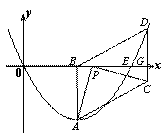
如图,抛物线y=ax2+bx+c经过原点,与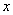 轴相交于点E(8, 0 ), 抛物线的顶点A在第四象限,点A到x轴的距离AB=4,点P(m, 0)是线段OE上一动点,连结PA,将线段PA绕点P逆时针旋转90°得到线段PC,过点C作y轴的平行线交x轴于点G,交抛物线于点D,连结BC和AD.
轴相交于点E(8, 0 ), 抛物线的顶点A在第四象限,点A到x轴的距离AB=4,点P(m, 0)是线段OE上一动点,连结PA,将线段PA绕点P逆时针旋转90°得到线段PC,过点C作y轴的平行线交x轴于点G,交抛物线于点D,连结BC和AD.
(1)求抛物线的解析式;
(2)求点C的坐标(用含m的代数式表示);
(3)当以点A、B、C、D为顶点的四边形是平行四边形时,求点P的坐标.
 |
(1)解:点E(8,0),AB⊥x轴,由抛物线的轴对称性可知B(4,0)点A(4,-4),抛物线经过点O(0,0),A(4,-4)、E(8,0)得,
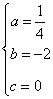
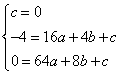
解得
 ∴抛物线的解析式为
∴抛物线的解析式为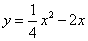
(2)解: ∵∠APC=90°∴∠APB+∠CPG=90°
∵AB⊥PE∴∠APB+∠PAB=90°
∴∠CPG=∠PAB
∵∠ABP=∠PGC=90°,PC=PA
∴△ABP≌△PGC
∴PB=CG,AB=PG=4 第26题 图1
∵P(m,0),OP=m ,且点P是线段OE上的动点
 ∴PB=CG=︱4-m︱, OG=︱m+4︱
∴PB=CG=︱4-m︱, OG=︱m+4︱
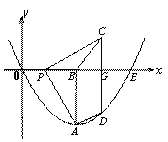
① 如图1,当点P在点B左边时,点C在x轴上方,
m<4,4-m>0,PB=CG=4-m
∴C(m+4,4-m)
②如图2,当点P在点B右边时,点C在x轴下方,
m>4,4-m<0,
∴PB=︱4-m︱=-(4-m)=m-4
∴CG=m-4 第26题 图2
∴C(m+4,4-m)
综上所述,点C坐标是C(m+4,4-m)
(3)解:如图1,当点P在OB上时
∵CD∥y轴,则CD⊥OE
∵点D在抛物线上,横坐标是m+4,将x= m+4代入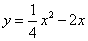 得
得

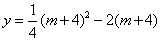
化简得: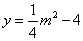
∴D(m+4,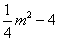 )
)
∴CD=4-m-(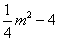 )=
)=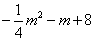
∵四边形ABCD是平行四边形 第26题 图1
∴AB=CD=4,
∴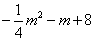 =4
=4
解得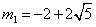 ,
,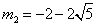
∵点P在线段OE上,∴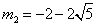 不符合题意,舍去
不符合题意,舍去
∴P(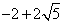 ,0)
,0)
如图2,当点P在线段BE上时,
∵C(m+4,4- m)
∵点D在抛物线上,横坐标是m+4,将x= m+4代入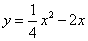 得
得
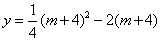
化简得: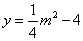
∴D(m+4,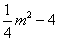 )
)
∴ CD=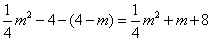
∵四边形ABDC是平行四边形 第26题 图2
∴AB=CD=4,
∴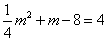
解得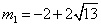 ,
,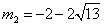
∵点P在线段OE上,∴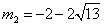 不符合题意,舍去
不符合题意,舍去
∴P(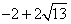 ,0)
,0)
综上所述,当以点A、B、C、D为顶点的四边形是平行四边形时,点P的坐标为
P(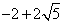 ,0)或P(
,0)或P(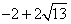 ,0)
,0)


 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:初中数学 来源: 题型:
在一个口袋中有4个完全相同的小球,把它们分别标号为①,②,③,④,随机地摸出一个小球,记录后放回,再随机摸出一个小球,则两次摸出的小球的标号相同的概率是( )
|
| A. |
| B. |
| C. |
| D. |
|
查看答案和解析>>
科目:初中数学 来源: 题型:
甲、乙两个商场出售相同的某种商品,每件售价均为3000元,并且多买都有一定的优惠.甲商场的优惠条件是:第一件按原售价收费,其余每件优惠30%;乙商场的优惠条件是:每件优惠25%.设所买商品为x件时,甲商场收费为y1元,乙商场收费为y2元.
(1)分别求出y1,y2与x之间的关系式;
(2)当甲、乙两个商场的收费相同时,所买商品为多少件?
(3)当所买商品为5件时,应选择哪个商场更优惠?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
在一次知识竞赛中,学校为获得一等奖和二等奖共30名学生购买奖品,共花费528元,其中一等奖奖品每件20元,二等奖奖品每件16元,求获得一等奖和二等奖的学生各有多少名?设获得一等奖的学生有x名,二等奖的学生有y名,根据题意可列方程组为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
某电视台为了了解本地区电视节目的收视率情况,对部分观众开展了“你最喜爱的电视节目”的问卷调查(每人只填写一项),根据收集的数据绘制了下面两幅不完整的统计图.根据要求回答下列问题:

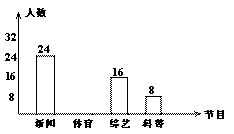
(1)本次问卷调查共调查了多少名观众?
(2)补全图1中的条形统计图;并求出图2中收看“综艺节目”的人数占调查总人数的百分比;
(3)求出图2中“科普节目”在扇形图中所对应的圆心角的度数;
(4) 现有喜欢“新闻节目”(记为A)、“体育节目”(记为B)、“综艺节目”(记为C)、“科普节目”(记为D)的观众各一名,电视台要从四人中随机抽取两人参加联谊活动,请用“列表法”或“画树形图”的方法求出恰好抽到喜欢“新闻节目”和“体育节目”两位观众的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,已知AB=AD,那么添加下列一个条件后,仍无法判定△ABC≌△ADC的是( )

A. CB=CD B. ∠BAC=∠DAC C. ∠BCA=∠DCA D. ∠B=∠D=90°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com