
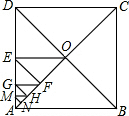
 如图,在正方形ABCD中,AO⊥BD、OE、FG、HM都垂直于AD,EF、GH、MN都垂直于AO,如果△AMN的面积为1,那么正方形ABCD的边长等于( )
如图,在正方形ABCD中,AO⊥BD、OE、FG、HM都垂直于AD,EF、GH、MN都垂直于AO,如果△AMN的面积为1,那么正方形ABCD的边长等于( )| A. | 8 | B. | 16 | C. | 12 | D. | 84或24 |
分析 根据题意知:△AMN,△MNH,△MHG,△GGF,△GFE,△EFO,△EOD都为等腰直角三角形,根据△AMN的面积为1,可求出MN的长,再根据等腰直角三角形的性质即可求出正方形ABCD的边长.
解答 解:在Rt△ANM中,
∵S△AMN=$\frac{1}{2}$(MN)2=1,
∴MN=$\sqrt{2}$,
在Rt△MNH中,MH=$\sqrt{2}$MN=2;
在Rt△MHG中,GH=$\sqrt{2}$MH=2$\sqrt{2}$;
在Rt△GHF中,GF=$\sqrt{2}$GH=4;
在Rt△GFE中,EF=$\sqrt{2}$GF=4$\sqrt{2}$;
在Rt△EFO中,OE=ED=$\sqrt{2}$EF=8;
∴AD=2ED=16
∴正方形ABCD的边长为16,
故选B.
点评 本题考查了正方形的性质,等腰直角三角形的性质,等腰三角形三线合一的性质,观察出下一次得到的三角形的边长是上一次三角形边长的$\sqrt{2}$倍是解题的关键.


科目:初中数学 来源: 题型:填空题
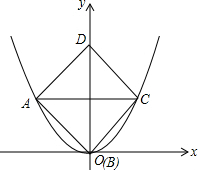 已知边长为2的正方形在平面直角坐标系中的位置如图所示,其顶点A、B、C在图中的抛物线上,则此抛物线的解析式为:$\frac{\sqrt{2}}{2}$x2.
已知边长为2的正方形在平面直角坐标系中的位置如图所示,其顶点A、B、C在图中的抛物线上,则此抛物线的解析式为:$\frac{\sqrt{2}}{2}$x2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
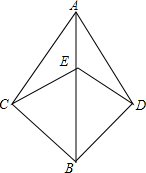 如图,AC=AD,BC=BD,点E在AB上.
如图,AC=AD,BC=BD,点E在AB上.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 圆周率π是无限不循环小数,它不是有理数 | |
| B. | 负整数与负分数统称为负有理数 | |
| C. | 正有理数与负有理数组成全体有理数 | |
| D. | $\frac{20}{5}$不是分数,而是整数 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com