练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    在同一平面上，若∠BOA=70°，∠BOC=15°，则∠AOC=
     
    ．
    考点：角的计算
    专题：分类讨论
    分析：在同一平面内，若∠BOA与∠BOC可能存在两种情况，即当OC在∠AOB的内部或OC在∠AOB的外部．
    解答：解：如图，当OC在∠AOB的内部时，∠AOC=∠BOA-∠BOC=55°，
    当OC在∠AOB的外部时，∠AOC=∠BOA+∠BOC=85°，
    故∠AOC的度数是55°或85°
    点评：考查了角的计算，解决本题的关键是意识到在同一平面内，∠BOA与∠BOC可能存在两种情况，即当OC在∠AOB的内部或OC在∠AOB的外部．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    将二次函数y=x2的图象向左平移1个单位，所得图象的函数关系式为（　　）
    A、y=x2+1
    B、y=x2-1
    C、y=（x+1）2
    D、y=（x-1）2

    查看答案和解析>>

    科目：初中数学 来源： 题型：

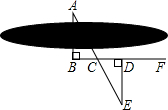    如图，要测量河岸相对两点A，B的距离，先在AB的垂线BF上取两点C、D，使CD=BC，再作出BF的垂线DE，使A、C、E在同一直线上，可以证明△EDC≌△ABC得ED=AB，因此测得DE的长度就是AB的长，判断△EDC≌△ABC的理由是（　　）
    A、边边边B、边角边
    C、角边角D、边边角

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    计算：
    （1）|-
    7
    2
    |×（
    1
    6
    -
    1
    2
    ）÷（-
    14
    3
    ）
    （2）（-1）6-
    1
    2
    ×[-2-（-3）2]+
    1
    2
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    已知△ABC的三个顶点的坐标分别为A（2，-1）、B（1，3）、C（-4，-2），求△ABC的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    二次函数y=ax2+bx+c的对称轴为x=1，与x轴的一个交点A在（2，0）和（3，0）之间，其部分图象如图，则下列结论正确的是（　　）
    A、b＜0B、ac＞0
    C、3a+c＞0D、3a+c＜0

    查看答案和解析>>

    科目：初中数学 来源： 题型：

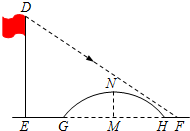    如图所示，该小组发现8米高旗杆DE的影子EF落在了包含一圆弧型小桥在内的路上，于是他们开展了测算小桥所在图的半径的活动．小刚身高1.6米，测得其影长为2.4米，同时测得EG的长为3米，HF的长为1米，测得拱高（弧GH的中点到弦GH的距离，即MN的长）为2米，则小桥所在圆的半径
     
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    设a1，a2，…，a2015是从1，0，-1这三个数组成的一列数，若a1+a2+…+a2015=70，（a1+1）2+（a2+1）2+…+（a2015+1）2=4005，则a1，a2，…，a2015中为0的数的个数是
     
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    在平面直角坐标系xOy中，A点的坐标为（6，3），在OA上有一点B，B点的横坐标为4，M为x轴上任意一点，当MA+MB取最小值时，M点的坐标为
     
    ．

    查看答案和解析>>

    同步练习册答案