
【题目】如图所示,在△ABC中, ![]() C=2
C=2 ![]() B,点D是BC上一点,AD=6,且AD
B,点D是BC上一点,AD=6,且AD ![]() AB,点E是BD上的点,AE=
AB,点E是BD上的点,AE= ![]() BD,AC=5,贝AB的长度为 .
BD,AC=5,贝AB的长度为 . 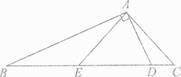
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,点D是等边△ABC中BC边上一点,过点D分别作DE∥AB,DF∥AC,交AC,AB于E,F,连接BE,CF,分别交DF,DE于点N,M,连接MN.试判断△DMN的形状,并说明理由.
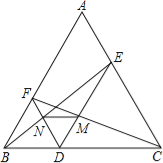
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探索函数![]() 的图象和性质.
的图象和性质.
已知函数y=x(x>0)和![]() 的图象如图所示,若P为函数
的图象如图所示,若P为函数![]() 图象上的点,过P作PC垂直于x轴且与直线、双曲线、x轴分别交于点A、B、C,则PC=
图象上的点,过P作PC垂直于x轴且与直线、双曲线、x轴分别交于点A、B、C,则PC= ![]() =AC+BC,从而“点P可以看作点A的沿竖直方向向上平移BC个长度单位(PA=BC)而得到”.
=AC+BC,从而“点P可以看作点A的沿竖直方向向上平移BC个长度单位(PA=BC)而得到”.
(1)根据以上结论,请在下图中作出函数![]() 图象上的一些点,并画出该函数的图象.
图象上的一些点,并画出该函数的图象.
(2)观察图象,写出函数![]() 两条不同类型的性质.
两条不同类型的性质.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人在一条长400米的直线跑道上同起点、同终点、同方向匀速跑步,先到终点的人原地休息.已知甲先出发3秒,在跑步过程中,甲、乙两人的距离y(米)与乙出发的时间t(秒)之间的关系如图所示,则下列结论正确的个数有( )
①乙的速度是4米/秒;
②离开起点后,甲、乙两人第一次相遇时,距离起点12米;
③甲从起点到终点共用时83秒;
④乙到达终点时,甲、乙两人相距68米;
⑤乙离开起点12秒后,甲乙第一次相遇.
A.4个
B.3个’
C.2个
D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 的图象与
的图象与![]() 轴交于点
轴交于点![]() ,与反比例函数
,与反比例函数![]() 的图象交于点
的图象交于点![]() .
.
(![]() )
)![]() __________;
__________;![]() __________.
__________.
(![]() )点
)点![]() 是直线
是直线![]() 上的动点(与点
上的动点(与点![]() ,
,![]() 不重合),过点
不重合),过点![]() 且平行于
且平行于![]() 轴的直线
轴的直线![]() 交这个反比例函数的图象于点
交这个反比例函数的图象于点![]() ,当点
,当点![]() 的横坐标为
的横坐标为![]() 时,得
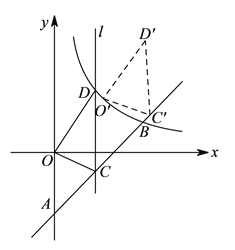
时,得![]() ,现将
,现将![]() 沿射线
沿射线![]() 方向平移一定的距离(如图),得到
方向平移一定的距离(如图),得到![]() ,若点
,若点![]() 的对应点
的对应点![]() 落在该反比例函数图象上,求点
落在该反比例函数图象上,求点![]() ,
,![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线l1:y1=x+m与直线l2:y2=nx+3相交于点A(1,2).
(1)求m、n的值;
(2)设l1交x轴于点B,l2交x轴于点C,若点D与点A,B,C能构成平行四边形,请直接写出D点坐标;
(3)请在所给坐标系中画出直线l1和l2 , 并根据图象回答问题:
当x满足时,y1>2;
当x满足时,0<y2≤3;
当x满足时,y1<y2 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com