
【题目】如图,在平行四边形![]() 中,
中,![]() 的平分线交
的平分线交![]() 于点E,交
于点E,交![]() 的延长线于F,以
的延长线于F,以![]() 为邻边作平行四边形
为邻边作平行四边形![]() 。
。
(1)证明平行四边形![]() 是菱形;
是菱形;
(2)若![]() ,连结
,连结![]() ,①求证:
,①求证:![]() ;②求
;②求![]() 的度数;
的度数;
(3)若![]() ,
,![]() ,
,![]() ,M是
,M是![]() 的中点,求
的中点,求![]() 的长。
的长。

【答案】(1)见解析;(2)①见解析;②∠BDG=60°;(3)![]()
【解析】
(1)平行四边形的性质可得AD∥BC,AB∥CD,再根据平行线的性质和角平分线的性质证明∠CEF=∠CFE,根据等角对等边可得CE=CF,再根据四边形ECFG是平行四边形,可得四边形ECFG为菱形;
(2)①根据已知和菱形的性质得出∠BEG=120°=∠DCG,再判断出AB=BE,进而得出BE=CD,即可判断出△BEG≌△DCG(SAS)
②先得出∠CGE=60°再由①得出△BDG是等边三角形,即可得出结论;
(3)首先证明四边形ECFG为正方形,再证明△BME≌△DMC可DM=BM,∠DMC=∠BME,再根据∠BMD=∠BME+∠EMD=∠DMC+∠EMD=90°可得到△BDM是等腰直角三角形,等腰直角三角形的性质即可得到结论.
解:(1)证明:∵AF平分∠BAD,
∴∠BAF=∠DAF,
∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥CD,
∴∠DAF=∠CEF,∠BAF=∠CFE,
∴∠CEF=∠CFE,
∴CE=CF,
又∵四边形ECFG是平行四边形,
∴四边形ECFG为菱形;
(2)①∵四边形ABCD是平行四边形,
∴AB∥DC,AB=DC,AD∥BC,
∵∠ABC=120°,
∴∠BCD=60°,∠BCF=120°
由(1)知,四边形CEGF是菱形,
∴CE=GE,∠BCG=![]() ∠BCF=60°,
∠BCF=60°,
∴CG=GE=CE,∠DCG=120°,
∵EG∥DF,
∴∠BEG=120°=∠DCG,
∵AE是∠BAD的平分线,
∴∠DAE=∠BAE,
∵AD∥BC,
∴∠DAE=∠AEB,
∴∠BAE=∠AEB,
∴AB=BE,
∴BE=CD,
∴△BEG≌△DCG(SAS),
②∵△BEG≌△DCG
∴BG=DG,∠BGE=∠DGC,
∴∠BGD=∠CGE,
∵CG=GE=CE,
∴△CEG是等边三角形,
∴∠CGE=60°,
∴∠BGD=60°,
∵BG=DG,
∴△BDG是等边三角形,
∴∠BDG=60°;
(3)连接BM,MC,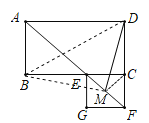
∵∠ABC=90°,四边形ABCD是平行四边形,
∴四边形ABCD是矩形,
又由(1)可知四边形ECFG为菱形,
∠ECF=90°,
∴四边形ECFG为正方形.
∵∠BAF=∠DAF,
∴BE=AB=DC,
∵M为EF中点,
∴∠CEM=∠ECM=45°,
∴∠BEM=∠DCM=135°,
在△BME和△DMC中,
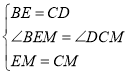
∴△BME≌△DMC(SAS),
∴MB=MD,
∠DMC=∠BME.
∴∠BMD=∠BME+∠EMD=∠DMC+∠EMD=90°,
∴△BMD是等腰直角三角形.
∵AB=8,AD=14,
∴BD=2![]() ,
,
![]()


科目:初中数学 来源: 题型:
【题目】如图,已知抛物线经过点A(﹣1,0)、B(3,0)、C(0,3)三点.
(1)求抛物线的解析式.
(2)点M是线段BC上的点(不与B,C重合),过M作MN∥y轴交抛物线于N,若点M的横坐标为m,请用m的代数式表示MN的长.
(3)在(2)的条件下,连接NB、NC,是否存在m,使△BNC的面积最大?若存在,求m的值;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校“体育课外活动兴趣小组”,开设了以下体育课外活动项目:A.足球 B.乒乓球C.羽毛球 D.篮球,为了解学生最喜欢哪一种活动项目,随机抽取了部分学生进行调查,并将调查结果绘制成了两幅不完整的统计图,请回答下列问题: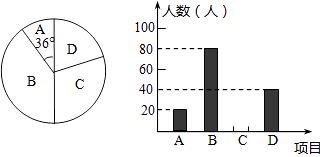
(1)这次被调查的学生共有人,在扇形统计图中“D”对应的圆心角的度数为;
(2)请你将条形统计图补充完整;
(3)在平时的乒乓球项目训练中,甲、乙、丙、丁四人表现优秀,现决定从这四名同学中任选两名参加市里组织的乒乓球比赛,求恰好选中甲、乙两位同学的概率(用树状图或列表法解答).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】五一小长假的某一天,亮亮全家上午![]() 时自驾小汽车从家里出发,到某旅游景点游玩,该小汽车离家的距离(千米)与时间(时)之间的关系如图所示,根据图像提供的有关信息,判断下列说法错误的是( )
时自驾小汽车从家里出发,到某旅游景点游玩,该小汽车离家的距离(千米)与时间(时)之间的关系如图所示,根据图像提供的有关信息,判断下列说法错误的是( )

A.景点离亮亮的家![]() 千米
千米
B.亮亮到家的时间为![]() 时
时
C.小汽车返程的速度为![]() 千米/时
千米/时
D.![]() 时至
时至![]() 时,小汽车匀速行驶
时,小汽车匀速行驶
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】垃圾的分类处理与回收利用,可以减少污染,节省资源.某城市环保部门为了提高宣传实效,抽样调查了部分居民小区一段时间内生活垃圾的分类情况,其相关信息如下:

根据图表解答下列问题:
(1)请将条形统计图补充完整;
(2)在扇形统计图样中,产生的有害垃圾C所对应的圆心角 度;
(3)调查发现,在可回收物中塑料类垃圾占13%,每回收1吨塑料类垃圾可获得0.5吨二级原料.假设该城市每月产生的生活垃圾为1000吨,且全部分类处理,那么每月回收的塑料类垃圾可以获得多少吨二级原料?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,从水平地面看一山坡上的通讯铁塔PC,在点A处用测角仪测得塔顶端点P的仰角是45°,向前走9m到达B点,用测角仪测得塔顶端点P和塔底端点C的仰角分别是60°和30°.
(1)求∠BPC的度数.
(2)求该铁塔PF的高度,(结果精确到0.1m,参考数据: ![]() .)
.)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某校在推进新课改的过程中,开设的体育选修课有:A:篮球,B:足球,C:排球,D:羽毛球,E:乒乓球,学生可根据自己的爱好选修一门,学校李老师对某班全班同学的选课情况进行调查统计,制成了两幅不完整的统计图(如图).
(1)请你求出该班的总人数,并补全频数分布直方图;
(2)该班班委4人中,1人选修篮球,2人选修足球,1人选修排球,李老师要从这4人中人任选2人了解他们对体育选课的看法,请你用列表或画树状图的方法,求选出的2人恰好1人选修篮球,1人选修足球的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形![]() 中,
中,![]() ,
,![]() 平分
平分![]() ,
,![]() 平分
平分![]() .
.
(1)如下图,求证:四边形![]() 是菱形;
是菱形;
(2)如下图,点![]() 为四边形
为四边形![]() 外一点,连接
外一点,连接![]() 、
、![]() 、
、![]() ,
,![]() 交
交![]() 于点
于点![]() ,
,![]() ,求证:
,求证:![]() ;
;
(3)如下图,在(2)的条件下,![]() ,点
,点![]() 为
为![]() 上一点,连接
上一点,连接![]() ,点
,点![]() 为
为![]() 延长线上一点,
延长线上一点,![]() ,连接
,连接![]() ,
,![]() 为
为![]() 上一点,连接
上一点,连接![]() ,若
,若![]() ,求
,求![]() 的值.
的值.
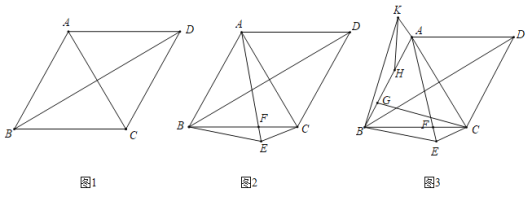
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com