
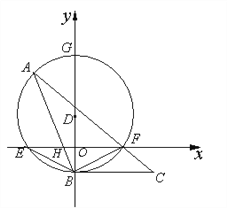
【题目】如图,在平面直角坐标中,点D在y轴上,以D为圆心,作⊙D交x轴于点E、F,交y轴于点B、G,点A在![]() 上,连接AB交x轴于点H,连接 AF并延长到点C,使∠FBC=∠A.
上,连接AB交x轴于点H,连接 AF并延长到点C,使∠FBC=∠A.
(1)判断直线BC与⊙D的位置关系,并说明理由;
(2)求证:BE2=BH·AB;
(3) 若点E坐标为(-4,0),点B的坐标为(0,-2),AB=8,求F与A两点的坐标.
【答案】(1)直线BC与⊙D相切,理由见解析;
(2)证明见解析;
(3)F(4,0),A(-4.8,4.4)
【解析】试题分析:(1)连FG,要证BC是切线,只需证∠DBC=90°,即证∠DBF+∠CBF=90°,而∠CBF=∠A,∠A=∠BGF,又∠BGF+∠DBF=90°,则可证明.
(2)连AE,则得到母子三角形的基本图形,结合垂径定理和圆周角定理证明△BEH∽△BAE即可.
(3)求坐标,作垂线,所以过点A分别向坐标轴作垂线,结合相似三角形的性质求出AQ,OQ的长即可.
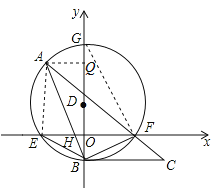
试题解析(1)直线BC与⊙D相切.
证明:如图,连接GF,∵BG是⊙D直径,∴∠GFB=90°.
∴∠G+∠GBF=90°,
∵∠A=∠G ,∠FBC=∠A,∴∠G=∠FBC,
∴∠FBC+∠GBF=90°,即∠GBC=90°,
∴直线BC与⊙D相切.
(2) 如图,连接AE.
∵BG⊥EF, BG是⊙D直径.
∴![]() ,∴∠BEH=∠BAE ,∵∠BAE=∠EAH , ∴△BEH∽△BAE.
,∴∠BEH=∠BAE ,∵∠BAE=∠EAH , ∴△BEH∽△BAE.
∴![]() ∴BE2=BH·AB.
∴BE2=BH·AB.
(3) 作AQ⊥GB,∵E(-4,0),根据垂径定理得,OE=OF=4,∴F(4,0) .
∵BE2=BH·AB, BE2=OE2 +OB2=16+4=20, AB=8,∴BH=2.5,得OH=1.5 .
由△BOH∽△BQA,得![]() AQ=4.8,BQ=6.4.
AQ=4.8,BQ=6.4.
∴OQ=4.4 ,∴A(-4.8,4.4).


科目:初中数学 来源: 题型:
【题目】用配方法解方程x2﹣6x﹣3=0,此方程可变形为( )
A. (x2﹣3)2=12B. (x+3)2=6
C. (x﹣3)2=12D. (x+3)2=9
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了考察甲、乙两块地小麦的长势,分别从中抽取10株苗,测得苗高如下(单位:cm):甲:12,13,14,15,10,16,13,11,15,11;乙:11,16,17,14,13,19,6,8,10,16.要比较哪块地小麦长得比较整齐,我们应选择的统计量是( )
A. 中位数B. 平均数C. 众数D. 方差
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方形AOBC在直角坐标系中,点A在y轴上,点B在x轴上,已知点C的坐标是(8,4).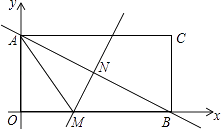
(1)求对角线AB所在直线的函数关系式;
(2)对角线AB的垂直平分线MN交x轴于点M,连接AM,求线段AM的长;
(3)若点P是直线AB上的一个动点,当△PAM的面积与长方形OABC的面积相等时,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下面推理过程: 如图,已知∠1=∠2,∠B=∠C,可推得AB∥CD.理由如下: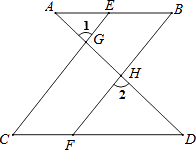
∵∠1=∠2(已知),
且∠1=∠CGD(),
∴∠2=∠CGD(等量代换).
∴CE∥BF().
∴∠=∠C().
又∵∠B=∠C(已知),
∴∠=∠B(等量代换).
∴AB∥CD().
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列二次函数中,图象以直线x=2为对称轴、且经过点(0,1)的是 ( )
A.y=(x-2)2+1B.y=(x+2)2+1
C.y=(x-2)2-3D.y=(x+2)2-3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】填写证明的理由.
已知:如图,AB∥CD,EF、CG分别是∠AEC、∠ECD的角平分线;求证:EF∥CG.
证明:∵AB∥CD(已知)
∴∠AEC=∠DCE ()
又∵EF平分∠AEC (已知)
∴∠1= ![]() ∠AEC ()
∠AEC ()
同理∠2= ![]() ∠DCE,∴∠1=∠2
∠DCE,∴∠1=∠2
∴EF∥CG ()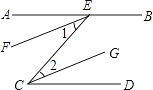
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com