
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
| 3 | 5 |
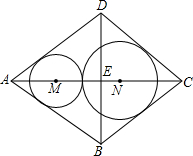 形零件(菱形铁片上只能加工同一直径的零件,不计加工过程中的损耗),问加工哪种零件能最充分地利用这种铁片并说明理由.
形零件(菱形铁片上只能加工同一直径的零件,不计加工过程中的损耗),问加工哪种零件能最充分地利用这种铁片并说明理由.查看答案和解析>>
科目:初中数学 来源:三点一测丛书九年级数学上 题型:044
两个多项式相除,可以先把这两个多项式都按照同一字母降幂排列,然后再仿照两个多位数相除的计算方法,用竖式进行计算.例如,我们来计算(7x+2+6x2)÷(2x+1),仿照672÷21,计算如下:

所以(7x+2+6x2)÷(2x+1)=3x+2.
由上面的计算可知计算步骤大体是:先用除式的第一项2x去除被除式的第一项6x2,得商式的第一项3x,然后用3x去乘除式,把积6x2+3x写在被除式下面(同类项对齐),从被除武中减去这个积,得4x+2,再把4x+2当作新的被除式,按照上面的方法继续计算,直到得出余式为止.上式的计算结果,余式等于0.如果一个多项式除以另一个多项式的余式为0,我们就说这个多项式能被另一个多项式整除,这时也可以说除式能整除被除式.
整式除法也有不能整除的情况.按照某个字母降幂排列的整式除法,当余式不是0而次数低于除式的次数时,除法计算就不能继续进行了,这说明除式不能整除被除式.例如,计算(9x2+2x3+5)÷(4x-3+x2).
解:
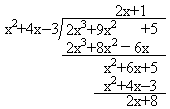
所以商式为2x+1,余式为2x+8.
与数的带余除法类似,上面的计算结果有下面的关系:9x2+2x3+5=(4x-3+x2)(2x+1)+(2x+8).这里应当注意,按照x的降幂排列,如果被除式有缺项,一定要留出空位.当然,也可用补0的办法补足缺项.
请你用上面的方法计算下面这道题:(6x3+x2-1)÷(2x-1).
查看答案和解析>>
科目:初中数学 来源:精编教材全解 数学 九年级上册 (配苏科版) 苏科版 题型:013
在一元二次方程ax2+bx+c=0(a≠0)中,如果a与c符号相异,那么方程( ).
A.有两个不相等的实数根
B.有两个相等的实数根
C.有一个实数根是0
D.没有实数根
查看答案和解析>>
科目:初中数学 来源:中华题王 数学 九年级上 (北师大版) 北师大版 题型:044
已知关于x的方程(k-1)x2+(2k-3)x+k+1=0有两个不相等的实数根x1,x2.
(1)求k的取值范围.
(2)是否存在实数k,使方程的两实数根互为相
反数?如果存在,求出k的值;如果不存在,请说明理由.
解:(1)根据题意,得
△=(2k-3)2-4(k-1)(k+1)
=4k2-12k+9-4k2+4
=-12k+13>0
∴k<![]()
∴k<![]() 时,方程有两个不相等的实数根.
时,方程有两个不相等的实数根.
(2)存在.如果方程的两个实数根互为相反数,则
x1+x2=![]() =0
=0
解得k=![]() .检验知,k=
.检验知,k=![]() 是
是![]() =0的解.
=0的解.
所以,当k=![]() 时,方程的两个实数根x1与x2互为相反数.
时,方程的两个实数根x1与x2互为相反数.
当你读了上面的解答过程后,请判断是否有错误?如果有,请指出错误之处,并直接写出正确的答案.
查看答案和解析>>
科目:初中数学 来源: 题型:单选题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com