
【题目】甲、乙两人匀速从同一地点到1500米处的图书馆看书,甲出发5分钟后,乙以50米/分的速度沿同一路线行走.设甲、乙两人相距s(米),甲行走的时间为t(分),s关于t的函数图象的一部分如图所示.
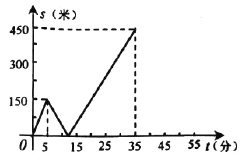
(1)求甲行走的速度;
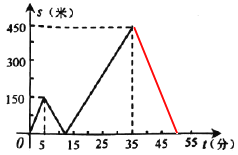
(2)在坐标系中,补画s关于t的函数图象的其余部分;
(3)问甲、乙两人何时相距360米?
【答案】(1)30米/分;(2)见解析;(3)当甲行走30.5分钟或38分钟时,甲、乙两人相距360米.
【解析】
(1)由图象可知t=5时,s=150米,根据速度=路程÷时间,即可解答;
(2)根据图象提供的信息,可知当t=35时,乙已经到达图书馆,甲距图书馆的路程还有(1500-1050)=450米,甲到达图书馆还需时间;450÷30=15(分),所以35+15=50(分),所以当s=0时,横轴上对应的时间为50.
(3)分别求出当12.5≤t≤35时和当35<t≤50时的函数解析式,根据甲、乙两人相距360米,即s=360,分别求出t的值即可.
(1)甲行走的速度:150÷5=30(米/分);
(2)当t=35时,甲行走的路程为:30×35=1050(米),乙行走的路程为:(35-5)×50=1500(米),
∴当t=35时,乙已经到达图书馆,甲距图书馆的路程还有(1500-1050)=450米,
∴甲到达图书馆还需时间;450÷30=15(分),
∴35+15=50(分),
∴当s=0时,横轴上对应的时间为50.
补画的图象如图所示(横轴上对应的时间为50),
(3)如图,
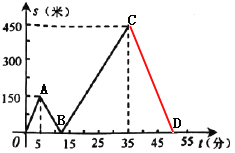
设乙出发经过x分和甲第一次相遇,根据题意得:150+30x=50x,
解得:x=7.5,
7.5+5=12.5(分),
由函数图象可知,当t=12.5时,s=0,
∴点B的坐标为(12.5,0),
当12.5≤t≤35时,设BC的解析式为:s=kt+b,(k≠0),
把C(35,450),B(12.5,0)代入可得:
![]()
解得:![]() ,
,
∴s=20t-250,
当35<t≤50时,设CD的解析式为s=k1x+b1,(k1≠0),
把D(50,0),C(35,450)代入得:
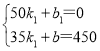
解得: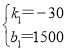
∴s=-30t+1500,
∵甲、乙两人相距360米,即s=360,
解得:t1=30.5,t2=38,
∴当甲行走30.5分钟或38分钟时,甲、乙两人相距360米.


 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:初中数学 来源: 题型:
【题目】在ABCD中,已知AB=6,BE平分∠ABC交AD边于点E,点E将AD分为1:3两部分,则AD的长为( )
A. 8或24B. 8C. 24D. 9或24
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某片果园有果树80棵,现准备多种一些果树提高果园产量,但是如果多种树,那么树之间的距离和每棵树所受光照就会减少,单棵树的产量随之降低,若该果园每棵果树产果y千克,增种果树x棵,它们之间的函数关系如图所示.

(1)求y与x之间的函数解析式;
(2)在投入成本最低的情况下,增种果树多少棵时,果园可以收获果实6750千克?
(3)当增种果树多少棵时,果园的总产量w(千克)最大?最大产量是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:∠AOB是一个直角,作射线OC,再分别作∠AOC和∠BOC的平分线OD、OE.
(1)如图①,当∠BOC=70°时,求∠DOE的度数;
(2)如图②,若射线OC在∠AOB内部绕O点旋转,当∠BOC=α时,求∠DOE的度数.
(3)如图③,当射线OC在∠AOB外绕O点旋转时,画出图形,直接写出∠DOE的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“龟兔赛跑”是同学们熟悉的寓言故事.如图所示,表示了寓言中的龟、兔的路程S和时间t的关系(其中直线段表示乌龟,折线段表示兔子).下列叙述正确的是( )

A. 赛跑中,兔子共休息了50分钟
B. 乌龟在这次比赛中的平均速度是0.1米/分钟
C. 兔子比乌龟早到达终点10分钟
D. 乌龟追上兔子用了20分钟
查看答案和解析>>
科目:初中数学 来源: 题型:
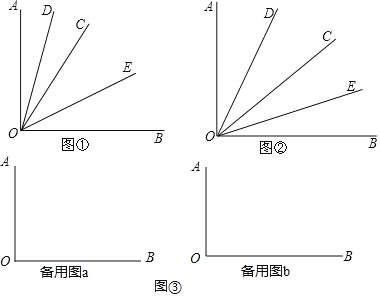
【题目】如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第1次从顶点运动到点(1,1),第2次接着运动到点(2,0),第3次接着运动到点(3,2),…按这样的运动规律,经过第2010次运动后,动点P的坐标是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一张长方形桌子可坐6人,按下图方式讲桌子拼在一起.
 ………
………
① ② ③
(1)观察图形,填写下表:
图形(n) | ② | ③ | …… | n |
坐的人数(人) | …… |
(2)一家餐厅有40张这样的长方形桌子,按照上图的方式每5张拼成1张大桌子,则40张桌子可拼成8张大桌子,共可坐多少人?
(3)在(2)中,若改为每8张桌子拼成1张大桌子,则共可坐多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
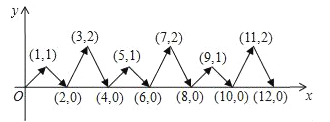
【题目】一农民带上若干千克自产的土豆进城出售,为了方便,他带了一些零钱备用,按市场价售出一些后,又降价出售,售出的土豆千克数与他手中持有的钱数(含备用零钱)的关系,如图所示,结合图象回答下列问题.
(1)农民自带的零钱是多少?
(2)试求降价前y与x之间的关系式
(3)由表达式你能求出降价前每千克的土豆价格是多少?
(4)降价后他按每千克0.4元将剩余土豆售完,这时他手中的钱(含备用零钱)是26元,试问他一共带了多少千克土豆?
查看答案和解析>>
科目:初中数学 来源: 题型:
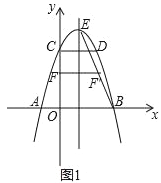
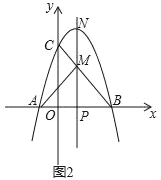
【题目】如图,二次函数y=﹣x2+bx+c的图象与x轴交于A、B两点,与y轴交于点C,OB=OC,点D在函数图象上,CD∥x轴且CD=2,直线l是抛物线的对称轴,E是抛物线的顶点.
(1)求b、c的值;
(2)如图1,连BE,线段OC上的点F关于直线l的对称点F’恰好在线段BE上,求点F的坐标;
(3)如图2,动点P在线段OB上,过点P作x轴的垂线分别与BC交于点M、与抛物线交于点N.试问:抛物线上是否存在点Q,使得△PQN与△APM的面积相等,且线段NQ的长度最小?若存在,求出点Q的坐标;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com