练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

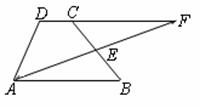
    如图，已知AB//DC，E是BC的中点，AE，DC的延长线交于点F；

    （1）求证：△ABE≌△FCE；

    （2）连接AC，BF．则四边形ABFC是什么特殊的四边形？请说明理由．



    证明：(1) ∵E是BC的中点     ∴BE=CE                  　

                 ∵AB//DC            ∴∠F=∠EAB, ∠FCE=∠B  　

                 ∴△ABE≌△FCE                                

    (2) ∵△ABE≌△FCE    ∴AE=FE                  　

    ∵BE=CE          ∴四边形ABFC是平行四边形.     


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    下列图形中阴影部分的面积相等的是

             

    A．② ③              B．③ ④              C．① ②              D．① ④

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    某汽车专卖店销售A，B两种型号的新能源汽车．上周售出1辆A型车和3辆B型车，销售额为96万元；本周已售2辆A型车和1辆B型车，销售额为62万元．

    (1)求每辆A型车和B型车的售价各多少万元．

    (2)甲公司拟向该店购买A，B两种型号的新能源汽车共6辆，购车费不少于130万元，且不超过140万元．则有哪几种购车方案?

    查看答案和解析>>

    科目：初中数学 来源： 题型：


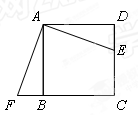
    如图，已知正方形ABCD的边长为12cm，E为CD边上一点，DE＝5cm．以点A为中心，将△ADE按顺时针方向旋转得△ABF，则点E所经过的路径长为               cm．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    解方程：

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    的倒数是(     )

    A．2        B．-2           C．       D．-

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，已知菱形ABCD的边长等于2，∠DAB=60°,则对角线BD的长为 (     )

    A． 1         B．    

    C． 2         D． 2

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    在平面直角坐标系中，我们不妨把横坐标和纵坐标相等的点叫“梦之点”，例如点（1,1），（-2，-2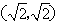），，…都是“梦之点”，显然“梦之点”有无数个。

    （1）若点P（2，m）是反比例函数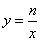（n为常数，n≠0）的图像上的“梦之点”，求这个反比例函数的解析式；

    （2）函数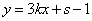（k,s为常数）的图像上存在“梦之点”吗？若存在，请求出“梦之点”的坐标，若不存在，说明理由；

    （3）若二次函数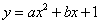（a,b是常数，a＞0）的图像上存在两个“梦之点”A，

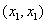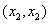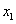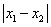    B,且满足-2＜＜2，=2，令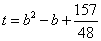，试求t的取值范围。

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    写出图象经过点（-1，1）的一个函数的解析式是   

    查看答案和解析>>

    同步练习册答案