
已知抛物线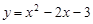 .
.
(1)它与x轴的交点的坐标为_______;
(2)在坐标系中利用描点法画出它的图象;
(3)将该抛物线在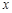 轴下方的部分(不包含与
轴下方的部分(不包含与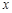 轴的交点)记为G,若直线
轴的交点)记为G,若直线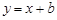 与G 只有一个公共点,则
与G 只有一个公共点,则 的取值范围是_______.
的取值范围是_______.
(1)(-1,0),(3,0)(2),列表,描点,连线及可画图。(3)-3≤b﹤1或b=-
解析试题分析:(1)∵y=x2-2x-3与x轴相交,y=0,∴x2-2x-3=0,解得x1=-1,x2=3.(2)图像的画法三步骤;列表,连点,连线。(3)∵y=x2-2x-3与y="x+b交于点G," ∴x2-2x-3="x+b" 即x2-3x-3-b="0∴△=9-4(-3-b),即21+4b≥0," ∴b≥- ,∵G点在x轴下面,∴x2-2x-3-b≤0 解得-3≤b<1解:(1)它与x轴的交点的坐标为(
,∵G点在x轴下面,∴x2-2x-3-b≤0 解得-3≤b<1解:(1)它与x轴的交点的坐标为( ,0),(3,0); 1分
,0),(3,0); 1分
(2)列表:
图象(如图);………………………… 3分x … 
0 1 2 3 … y … 0 


0 …
(3) 的取值范围是
的取值范围是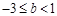 或
或 .…5分
.…5分
阅卷说明:只写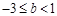 或只写
或只写 得1分.
得1分.
考点:二次函数图像的性质,图像的画法,
点评:由解析式与x轴相交纵坐标为0,解方程可求出坐标点,根据解析式,可画图像,由于一次函数与二次函数有唯一交点,可列方程,点G又在x轴下,构建不等式求出b的取值范围。属于中档题,注意的是,构建不等式及其解法。


 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案科目:初中数学 来源: 题型:
| 7 | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 已知抛物线y=-
已知抛物线y=-| 1 | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 的抛物线y=ax2,求原二次函数的解析式.
的抛物线y=ax2,求原二次函数的解析式.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
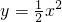 ,把它平移后得抛物线C2,使C2经过点A(0,8),且与抛物线C1交于点B(2,n).在x轴上有一点P,从原点O出发以每秒1个单位的速度沿x轴正半轴的方向移动,设点P移动的时间为t秒,过点P作x轴的垂线l,分别交抛物线C1、C2于E、D,当直线l经过点B前停止运动,以DE为边在直线l左侧画正方形DEFG.
,把它平移后得抛物线C2,使C2经过点A(0,8),且与抛物线C1交于点B(2,n).在x轴上有一点P,从原点O出发以每秒1个单位的速度沿x轴正半轴的方向移动,设点P移动的时间为t秒,过点P作x轴的垂线l,分别交抛物线C1、C2于E、D,当直线l经过点B前停止运动,以DE为边在直线l左侧画正方形DEFG.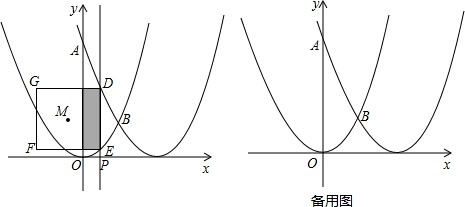
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com