
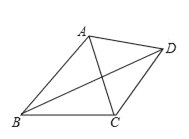
【题目】如图,已知四边形ABCD中,对角线BD平分∠ABC,∠ADB=32°,∠BCD+∠DCA=180°,那么∠ACD为_____度.
【答案】58.
【解析】
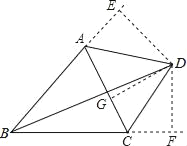
延长BA和BC,过D点作DE⊥BA于E点,过D点作DF⊥BC于F点,根据BD是∠ABC的平分线可得出DE=DF,过D点作DG⊥AC于G点,进而得出CD为∠ACF的平分线,设∠ABD=x°,则∠ABC=2x°,∠EAD=∠ABD+∠ADB=x°+32°,再根据∠BAE+∠BCF=360°,即可得出结论.
延长BA和BC,过D点作DE⊥BA于E点,过D点作DF⊥BC于F点,过D点作DG⊥AC于G点,
∵BD是∠ABC的平分线,
∴DE=DF,
又∵∠BCD+∠DCA=180°,
∠BCD+∠DCF=180°,
∴∠ACD=∠DCF,
∴DG=DF=DE
∴AD为∠EAC的平分线,
设∠ABD=x°,则∠ABC=2x°,∠EAD=∠ABD+∠ADB=x°+32°,
∵∠BAE+∠BCF=360°,
∴2(x°+32°)+∠BAC+∠ACB+2∠ACD=360°,
2x°+64°+180°﹣2x°+2∠ACD=360°,
∠ACD=58°.
故答案为:58.


 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:初中数学 来源: 题型:
【题目】某养鸡场有2500只鸡准备对外出售.从中随机抽取了一部分鸡,根据它们的质量(单位:![]() ),绘制出如下的统计图①和图②.请根据相关信息,解答下列问题:
),绘制出如下的统计图①和图②.请根据相关信息,解答下列问题:

(Ⅰ)图①中![]() 的值为 ;
的值为 ;
(Ⅱ)求统计的这组数据的平均数、众数和中位数;
(Ⅲ) 根据样本数据,估计这2500只鸡中,质量为![]() 的约有多少只?
的约有多少只?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形OABC的一边OA在x轴的负半轴上,O是坐标原点,tan∠AOC=![]() ,反比例函数y=
,反比例函数y=![]() 的图象经过点C,与AB交于点D,若△COD的面积为20,则k的值等于_____.
的图象经过点C,与AB交于点D,若△COD的面积为20,则k的值等于_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
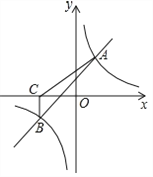
【题目】如图,一次函数![]() 与反比例函数
与反比例函数![]() 的图象交于A(2,3),B(-3,n)两点.
的图象交于A(2,3),B(-3,n)两点.
(1)求一次函数与反比例函数的表达式;
(2)根据所给条件,请直接写出不等式![]() <
<![]() 的解集;
的解集;
(3)过点B作BC⊥x轴,垂足为C,求S△ABC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠C=90°,AC=BC=4,将△ABC翻折,使得点A落在BC的中点A'处,折痕分别交边AB、AC于点D、点E,那么AD:AE的值为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有四种运算程序如下图所示,按要求完成下列题:
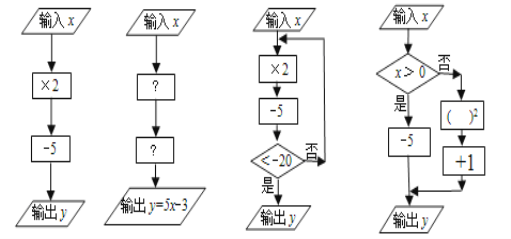
(1)如图1,当输入数x=-2时,输出数y=_______ ;
(2)如图2,第一个带?号的运算框内,应填_______ ;第二个带?号运算框内,应填_______ ;
(3)如图3,当输入数x=1时,输出数y= _______;
(4)如图4,当输出的值y=26,则输入的值x=_______ .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小红驾车从甲地到乙地.设她出发第x h时距离乙地y km,图中的折线表示她在整个驾车过程中y与x之间的函数关系.
(1)①已知小丽驾车中途休息了1小时,则B点的坐标为(_______,______);
②求线段AB所表示的y与x之间的函数关系式;
(2)从图象上看,线段AB比线段CD“陡”,请说明它表示的实际意义.

查看答案和解析>>
科目:初中数学 来源: 题型:
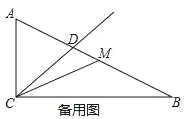
【题目】如图,已知△ABC中,∠ACB=90°,AC=1,BC=2,CD平分∠ACB交边AB与点D,P是射线CD上一点,联结AP.
(1)求线段CD的长;
(2)当点P在CD的延长线上,且∠PAB=45°时,求CP的长;
(3)记点M为边AB的中点,联结CM、PM,若△CMP是等腰三角形,求CP的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com