
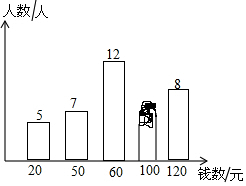
 小明调查了学校50名同学本学期购买课外书的花费情况,并将结果绘制成了下面的统计图,由于不小心滴上了墨水,导致花费为100元的人数看不清楚了.求出这50名学生本学期购买课外书花费的众数、中位数和平均数.
小明调查了学校50名同学本学期购买课外书的花费情况,并将结果绘制成了下面的统计图,由于不小心滴上了墨水,导致花费为100元的人数看不清楚了.求出这50名学生本学期购买课外书花费的众数、中位数和平均数.  仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案科目:初中数学 来源: 题型:解答题
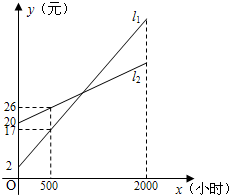 如图所示,L1,L2分别表示一种白炽灯和一种节能灯的费用y(费用=灯的售价+电费,单位:元)与照明时间x(h)的函数关系图象,假设两种灯的使用寿命都是2000h,照明效果一样.
如图所示,L1,L2分别表示一种白炽灯和一种节能灯的费用y(费用=灯的售价+电费,单位:元)与照明时间x(h)的函数关系图象,假设两种灯的使用寿命都是2000h,照明效果一样.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
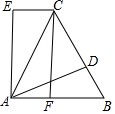 如图,△ABC是等边三角形,D是BC上一点,△ABD经旋转后到达△ACE的位置.
如图,△ABC是等边三角形,D是BC上一点,△ABD经旋转后到达△ACE的位置.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在同一平面直角坐标系内画一次函数y1=-x+4和y2=2x-5的图象,根据图象求:
在同一平面直角坐标系内画一次函数y1=-x+4和y2=2x-5的图象,根据图象求:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
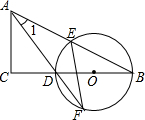 如图,△ABC中,∠C=90°,D是BC边上一点,以DB为直径的⊙O交AB于E,交AD的延长线于F,连结EF,∠1=∠F.
如图,△ABC中,∠C=90°,D是BC边上一点,以DB为直径的⊙O交AB于E,交AD的延长线于F,连结EF,∠1=∠F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
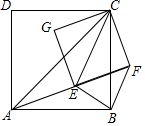 如图,已知AC、EC分别为四边形ABCD和EFCG的对角线,点E在△ABC内,∠CAE+∠CBE=90°,当四边形ABCD和EFCG均为正方形时,连接BF.
如图,已知AC、EC分别为四边形ABCD和EFCG的对角线,点E在△ABC内,∠CAE+∠CBE=90°,当四边形ABCD和EFCG均为正方形时,连接BF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 分别画出满足下列条件的点:(尺规作图,请保留组图痕迹,不写作法).
分别画出满足下列条件的点:(尺规作图,请保留组图痕迹,不写作法).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,直线y=ax-4(a≠0)与双曲线y=$\frac{k}{x}$只有一个公共点A(1,-2).
如图,直线y=ax-4(a≠0)与双曲线y=$\frac{k}{x}$只有一个公共点A(1,-2).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com