练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    18．如图所示，OA、OB是两条相交的高速公路，C、D是两处村庄，某百货集团响应新农村建设的要求，要在高速路内建一座大型便民超市P，使PC=PD，且P到∠AOB的两边OA、OB的距离相等，那么超市P的位置应选在哪里？

    分析 利用线段垂直平分线的性质结合角平分线的性质得出其交点P的位置．

    解答 解：如图所示：点P即为所求．

    点评 此题主要考查了角平分线的性质以及线段垂直平分线的性质以及其作法，正确应用相关性质是解题关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    8．下列计算正确的是（　　）
    A．（-2）-（-5）=-7B．（+3）+（-6）=3C．（+5）-（-8）=-3D．（-5）-（-8）=3

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    9．如图，DE∥BC，且S△DOE：S△BOC=4：9，则S△ADE：S△EDC等于（　　）
    A．2：3B．3：2C．2：1D．1：2

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

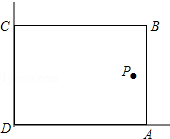    6．在美化校园的活动中，某兴趣小组想借助如图所示的直角墙角（两边足够长），用28m长的篱笆围成一个矩形花园ABCD（篱笆只围AB，BC两边），设AB=x（m）．
    （1）若花园的面积为187m2，求x的值；
    （2）若在P处有一棵树与墙CD，AD的距离分别是16m和6m，要将这棵树围在花园内（含边界，不考虑树的粗细），求花园面积S的最大值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

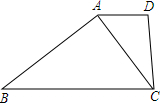    13．如图，AD∥BC，∠B=∠DCA．
    （1）证明△ABC∽△DCA，并写出对应边的比例式；
    （2）若AB=10，BC=12，CA=6．求AD、DC的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    3．如图，抛物线y=-x2+4ax-3经过点M（2，1），交x轴于A、B，交y轴负半轴于C，平移CM交x轴于D，交对称轴右边的抛物线于P，使DP=CM，求点P的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

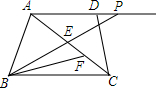    10．已知，如图，在梯形ABCD中，AD∥BC，BC=6，点P是射线AD上的点，BP交AC于点E，∠CBP的角平分线交AC于点F，且CF=$\frac{1}{3}$AC时．求AP+BP的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    3．如图，从点A（2，0）发出的一束光，经y轴反射，过点C（3，5），则B点的坐标为（0，2）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    4．阅读探索：
    （1）若a＞b，b＞c，则a，c的大小关系是a＞c．若a≥b，b≥c，则a，c的大小关系是a≥c．若a≥b，b＞c，则a，c的大小关系是a＞c．
    拓展提高：
    （2）已知a＞b，m＞n，试比较a+m与b+n的大小，并结合上述规律说明理由．
    能力运用：
    （3）已知x，y满足-2≤x+y≤4，0≤2x-y＜8，分别求出x，y的取值范围．

    查看答案和解析>>

    同步练习册答案