
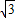 ;②用一组与背水坡面长边垂直的平行线将背水坡面分成9块相同的矩形区域,依次相间地种草与栽花.
;②用一组与背水坡面长边垂直的平行线将背水坡面分成9块相同的矩形区域,依次相间地种草与栽花.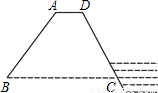
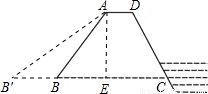 解:(1)作AE⊥BC于E.
解:(1)作AE⊥BC于E.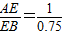 =
= ,
,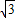 ,有tan∠AB′E=
,有tan∠AB′E= ,
, =80米2,
=80米2,

科目:初中数学 来源: 题型:
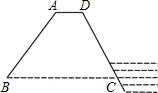 一座建于若干年前的水库大坝的横断面如图所示,其中背水面的整个坡面是长为90米、宽为5米的矩形.现需将其整修并进行美化,方案如下:①将背水坡AB的坡度由1:0.75改为1:
一座建于若干年前的水库大坝的横断面如图所示,其中背水面的整个坡面是长为90米、宽为5米的矩形.现需将其整修并进行美化,方案如下:①将背水坡AB的坡度由1:0.75改为1:| 3 |
查看答案和解析>>
科目:初中数学 来源:四川省中考真题 题型:解答题
 ;②用一组与背水坡面长边垂直的平行线将背水坡面分成9块相同的矩形区域,依次相间地种草与栽花。
;②用一组与背水坡面长边垂直的平行线将背水坡面分成9块相同的矩形区域,依次相间地种草与栽花。
查看答案和解析>>
科目:初中数学 来源:第1章《解直角三角形》常考题集(16):1.3 解直角三角形(解析版) 题型:解答题
 ;②用一组与背水坡面长边垂直的平行线将背水坡面分成9块相同的矩形区域,依次相间地种草与栽花.
;②用一组与背水坡面长边垂直的平行线将背水坡面分成9块相同的矩形区域,依次相间地种草与栽花.
查看答案和解析>>
科目:初中数学 来源:第28章《锐角三角函数》常考题集(16):28.2 解直角三角形(解析版) 题型:解答题
 ;②用一组与背水坡面长边垂直的平行线将背水坡面分成9块相同的矩形区域,依次相间地种草与栽花.
;②用一组与背水坡面长边垂直的平行线将背水坡面分成9块相同的矩形区域,依次相间地种草与栽花.
查看答案和解析>>
科目:初中数学 来源:第25章《解直角三角形》常考题集(13):25.3 解直角三角形(解析版) 题型:解答题
 ;②用一组与背水坡面长边垂直的平行线将背水坡面分成9块相同的矩形区域,依次相间地种草与栽花.
;②用一组与背水坡面长边垂直的平行线将背水坡面分成9块相同的矩形区域,依次相间地种草与栽花.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com