
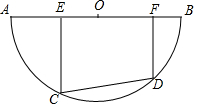
 如图,半圆O的直径AB=10,有一条定长为6的动弦CD在弧AB上滑动(点C、点D分别不与点A、点B重合),点E、F在AB上,EC⊥CD,FD⊥CD.
如图,半圆O的直径AB=10,有一条定长为6的动弦CD在弧AB上滑动(点C、点D分别不与点A、点B重合),点E、F在AB上,EC⊥CD,FD⊥CD.分析 (1)过点O作OH⊥CD于H,由垂径定理得出CH=DH,证得EC∥OH∥FD,即可得出结论;
(2)由勾股定理求出OH=$\sqrt{O{C}^{2}-C{H}^{2}}$═4,由平行线的性质得出∠ECO=∠COH≠45°;分两种情况讨论:
①当∠EOC=45°时,过点E作EM⊥OC于M,则△OEM是等腰直角三角形,得出EM=OM,证明△ECM∽△COH,得出EM:CM=CH:OH=3:4.设EM=3m,CM=4m.则OM=3m,EO=$\sqrt{2}$OM=3$\sqrt{2}$m,由CM+OM=OC,得出方程4m+3m=5,解方程得出m=$\frac{5}{7}$,即可得出EO=$\frac{15\sqrt{2}}{7}$,EF=2EO=$\frac{30\sqrt{2}}{7}$.
②当∠CEO=45°时,过点O作ON⊥EC于N;.在Rt△CON中,ON=CH=3,CN=OH=4.在Rt△EON中,EO=3$\sqrt{2}$.得出EF=2OE=6$\sqrt{2}$即可.
(3)证明OH是梯形EFDC的中位线,由梯形中位线定理得出EC+FD=2OH=8,由梯形面积公式得出S=$\frac{1}{2}$(EC+FD)•CD=OH•CD=244×6=24(0<x<8);作FG⊥EC于G,则GC=FD=8-x,GF=CD=6,求出EG=EC-GC=2x-8,由勾股定理得出EF=$\sqrt{E{G}^{2}+F{G}^{2}}$=2$\sqrt{{x}^{2}-8x+25}$,得出四边形CDFE周长l=EF+EC+CD+FD=EF+2OH+CD=2$\sqrt{{x}^{2}-8x+25}$+14(0<x<8).
解答 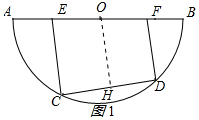 (1)证明:过点O作OH⊥CD于H,如图所示:
(1)证明:过点O作OH⊥CD于H,如图所示:
则CH=DH,
∵EC⊥CD,FD⊥CD,OH⊥CD,
∴EC∥OH∥FD,
∵CH=DH,
∴EO=FO;
(2)解:∵OH⊥CD,OC=$\frac{1}{2}$AB=5,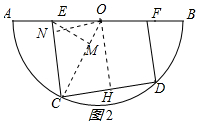
∴CH=$\frac{1}{2}$CD=3,
∴OH=$\sqrt{O{C}^{2}-C{H}^{2}}$=$\sqrt{{5}^{2}-{3}^{2}}$=4,
∵EC∥OH,
∴∠ECO=∠COH≠45°;
①当∠EOC=45°时,过点E作EM⊥OC于M,
则△OEM是等腰直角三角形,
∴EM=OM,
∵∠ECM=∠COH,∠CME=∠OHC=90°,
∴△ECM∽△COH,
∴EM:CM=CH:OH=3:4.
在Rt△ECM中,设EM=3m,CM=4m.则OM=3m,EO=$\sqrt{2}$OM=3$\sqrt{2}$m,
∵CM+OM=OC,
∴4m+3m=5,
解得:m=$\frac{5}{7}$,
∴EO=$\frac{15\sqrt{2}}{7}$,
EF=2EO=$\frac{30\sqrt{2}}{7}$.
②当∠CEO=45°时,过点O作ON⊥EC于N;.
在Rt△CON中,ON=CH=3,CN=OH=4.
在Rt△EON中,EO=3$\sqrt{2}$.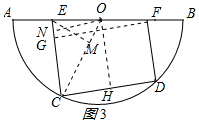
∴EF=2OE=6$\sqrt{2}$.
综上所述,线段EF的长等于$\frac{30\sqrt{2}}{7}$或6$\sqrt{2}$.
(3)解:四边形CDFE的面积S不随变量x的变化而变化,是一个不变量;
四边形CDFE的周长l随变量x的变化而变化.理由如下:
由①得:EO=FO,CH=DH,
∴OH是梯形EFDC的中位线,
∴EC+FD=2OH=8,
∴四边形CDFE面积为S=$\frac{1}{2}$(EC+FD)•CD=OH•CD=4×6=24(0<x<8)(是一个常值函数);
作FG⊥EC于G,则GC=FD=8-x,GF=CD=6,
∴EG=EC-GC=x-(8-x)=2x-8,
∴EF=$\sqrt{E{G}^{2}+F{G}^{2}}$=$\sqrt{(2x-8)^{2}+{6}^{2}}$=2$\sqrt{{x}^{2}-8x+25}$,
∴四边形CDFE周长l=EF+EC+CD+FD=EF+2OH+CD=2$\sqrt{{x}^{2}-8x+25}$+14(0<x<8),
即l═2$\sqrt{{x}^{2}-8x+25}$+14(0<x<8).
点评 本题是圆的综合题目,考查了垂径定理、勾股定理、平行线的性质、梯形中位线定理、等腰直角三角形的判定与性质、梯形面积的计算等知识;本题综合性强,有一定难度.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
 小赵和小王交流暑假中的活动,小赵说:“我们一家外出旅行了一个星期,这7天的日期数之和是84天,你知道我们几号出去的么?”小王说“我暑假去舅舅家住了7天,日历数再加月份数也是84,你能猜出我是几月几号回的家?试试看列出方程,解决小赵、小王的问题.(提示:7月1日-9月1日暑假)
小赵和小王交流暑假中的活动,小赵说:“我们一家外出旅行了一个星期,这7天的日期数之和是84天,你知道我们几号出去的么?”小王说“我暑假去舅舅家住了7天,日历数再加月份数也是84,你能猜出我是几月几号回的家?试试看列出方程,解决小赵、小王的问题.(提示:7月1日-9月1日暑假)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
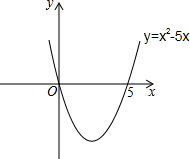 自主学习,请阅读下列解题过程.
自主学习,请阅读下列解题过程.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
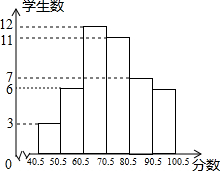 某班学生参加环保知识竞赛,已知竞赛得分都是整数.把参赛学生的成绩整理后分为6小组,画出竞赛成绩的频数分布直方图(如图所示),根据图中的信息,可得成绩高于60分的学生占全班参赛人数的百分率是80%.
某班学生参加环保知识竞赛,已知竞赛得分都是整数.把参赛学生的成绩整理后分为6小组,画出竞赛成绩的频数分布直方图(如图所示),根据图中的信息,可得成绩高于60分的学生占全班参赛人数的百分率是80%.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com