Question

如图，BC∥DE，AB：AD=1：3，则S_△ABC：S_{四边形BDEC}=    ．

Answer 1

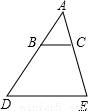
【答案】分析：由于BC∥DE，利用平行线分线段成比例定理的推论可知△ABC∽△ADE，再利用相似三角形面积比等于相似比的平方易求S_△ABC：S_△ADE=1：9，从而易求S_△ABC：S_{四边形BDEC}=1：8．
解答：解：∵BC∥DE，
∴△ABC∽△ADE，
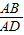
∴S_△ABC：S_△ADE=（）²，
又∵AB：AD=1：3，
∴S_△ABC：S_△ADE=1：9，
∴S_△ABC：S_{四边形BDEC}=1：8．
故答案是1：8．
点评：本题考查了本题考查了相似三角形的判定和性质、平行线分线段成比例定理的推论．相似三角形面积比等于相似比的平方．