
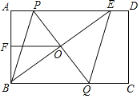
【题目】如图,在矩形ABCD中,E是AD上一点,PQ垂直平分BE,分别交AD,BE,BC于点P,O,Q,连接BP,EQ.
(1)求证:四边形BPEQ是菱形;
(2)F为AB的中点,则线段OF与线段AE有什么位置关系和数量关系,并说明理由;
(3)在(2)的条件下,若AB=6,OF=4,求PQ的长.
【答案】(1)见解析;(2)见解析;(3)PQ=![]() .
.
【解析】
(1)先根据线段垂直平分线的性质证明QB=QE,由ASA证明△BOQ≌△EOP,得出PE=QB,证出四边形BPEQ是平行四边形,再根据菱形的判定即可得出结论;
(2)根据中位线定理即可求出线段OF与线段AE的位置关系和数量关系.
(3)根据勾股定理求出OB的长度,进而求出BE, 设菱形的边长为x,则AP=8﹣x.
在Rt△APB中,根据勾股定理列出方程,求出边长,根据菱形的面积公式进行求解即可.
(1)证明:∵PQ垂直平分BE,
∴PB=PE,OB=OE,
∵四边形ABCD是矩形,
∴AD∥BC,
∴∠PEO=∠QBO,
在△BOQ与△EOP中,∠PEO=∠QBO,OB=OE,∠POE=∠QOB,
∴△BOQ≌△EOP(ASA),
∴PE=QB,
又∵AD∥BC,
∴四边形BPEQ是平行四边形,
又∵QB=QE,
∴四边形BPEQ是菱形;
(2)∵四边形BPEQ是菱形,
∴OB=OE.
又∵F是AB的中点,
∴OF是△BAE的中位线,
∴AE∥OF且OF=![]() AE.
AE.
(3)∵AB=6,F是AB的中点,
∴BF=3.
∵OF∥AE,
∴∠BFO=90°.
在Rt△FOB中, ![]()
∴BE=10.
设菱形的边长为x,则AP=8﹣x.
在Rt△APB中,BP2=AB2+AP2,即x2=62+(8﹣x)2,解得:x=![]() .
.
由菱形的面积公式可知: ![]() 解得:PQ
解得:PQ![]()


科目:初中数学 来源: 题型:
【题目】对于平面直角坐标系xOy中的点![]() ,若点
,若点![]() 的坐标为
的坐标为![]() (其中k为常数,且
(其中k为常数,且![]() ),则称点
),则称点![]() 为点P的“k属派生点”.
为点P的“k属派生点”.
例如:![]() 的“4属派生点”为
的“4属派生点”为![]() ,即
,即![]() .
.
(1)点![]() 的“2属派生点”
的“2属派生点”![]() 的坐标为________;
的坐标为________;
(2)若点P的“3属派生点”![]() 的坐标为
的坐标为![]() ,求点P的坐标;
,求点P的坐标;
(3)若点P在y轴的正半轴上,点P的“k属派生点”为![]() 点,且点
点,且点![]() 到y轴的距离不小于线段OP长度的5倍,则k的取值范围是________________.
到y轴的距离不小于线段OP长度的5倍,则k的取值范围是________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
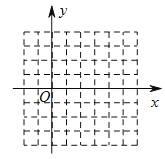
【题目】请在网格坐标系中画出二次函数![]() 的大致图象(注:图中小正方形网格的边长为
的大致图象(注:图中小正方形网格的边长为![]() ),根据图象填空:
),根据图象填空:
(![]() )当
)当![]() __________时,
__________时,![]() 有最__________值
有最__________值![]() __________.
__________.
(![]() )
)![]() 随
随![]() 的增大而减小的自变量
的增大而减小的自变量![]() 的取值范围是__________.
的取值范围是__________.
(![]() )结合图象直接写出
)结合图象直接写出![]() 时
时![]() 的范围:__________.
的范围:__________.
(![]() )结合图象直接写出
)结合图象直接写出![]() 时
时![]() 的取值范围:__________.
的取值范围:__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
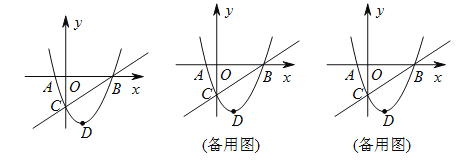
【题目】如图,在平面直角坐标系中,二次函数![]() 的图像与
的图像与![]() 轴交于
轴交于![]() 、
、![]() 两点,与
两点,与![]() 轴交于
轴交于![]() 点,点
点,点![]() 是抛物线顶点,点
是抛物线顶点,点![]() 是直线
是直线![]() 下方的抛物线上一动点.
下方的抛物线上一动点.
(![]() )这个二次函数的表达式为____________.
)这个二次函数的表达式为____________.
(![]() )设直线
)设直线![]() 的解析式为
的解析式为![]() ,则不等式
,则不等式![]() 的解集为___________.
的解集为___________.
(![]() )连结
)连结![]() 、
、![]() ,并把
,并把![]() 沿
沿![]() 翻折,得到四边形
翻折,得到四边形![]() ,那么是否存在点
,那么是否存在点![]() ,使四边形
,使四边形![]() 为菱形?若存在,请求出此时点
为菱形?若存在,请求出此时点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
(![]() )当四边形
)当四边形![]() 的面积最大时,求出此时
的面积最大时,求出此时![]() 点的坐标和四边形
点的坐标和四边形![]() 的最大面积.
的最大面积.
(![]() )若把条件“点
)若把条件“点![]() 是直线
是直线![]() 下方的抛物线上一动点.”改为“点
下方的抛物线上一动点.”改为“点![]() 是抛物线上的任一动点”,其它条件不变,当以
是抛物线上的任一动点”,其它条件不变,当以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形为梯形时,直接写出点
为顶点的四边形为梯形时,直接写出点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
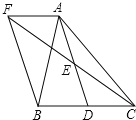
【题目】如图,在![]() 中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线交CE的延长线于点F,且
中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线交CE的延长线于点F,且![]() ,连接BF.
,连接BF.
![]() 证明:
证明:![]() ;
;
![]() 当
当![]() 满足什么条件时,四边形AFBD是矩形?并说明理由.
满足什么条件时,四边形AFBD是矩形?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数轴上![]() 、
、![]() 两点对应的有理数分別为
两点对应的有理数分別为![]() 和
和![]() ,点
,点![]() 和点
和点![]() 分别同时从点
分别同时从点![]() 和点
和点![]() 出发,以每秒
出发,以每秒![]() 个单位长度,每秒
个单位长度,每秒![]() 个单位长度的速度向数轴正方向运动,设运动时间为
个单位长度的速度向数轴正方向运动,设运动时间为![]() 秒.
秒.
![]()
(1)当![]() 时,则
时,则![]() 、
、![]() 两点对应的有理数分别是______;
两点对应的有理数分别是______;![]() _______;
_______;
(2)点![]() 是数轴上点
是数轴上点![]() 左侧一点,其对应的数是
左侧一点,其对应的数是![]() ,且
,且![]() ,求
,求![]() 的值;
的值;
(3)在点![]() 和点
和点![]() 出发的同时,点
出发的同时,点![]() 以每秒
以每秒![]() 个单位长度的速度从点
个单位长度的速度从点![]() 出发,开始向左运动,遇到点
出发,开始向左运动,遇到点![]() 后立即返回向右运动,遇到点
后立即返回向右运动,遇到点![]() 后立即返回向左运动,与点
后立即返回向左运动,与点![]() 相遇后再立即返回,如此往返,直到
相遇后再立即返回,如此往返,直到![]() 、
、![]() 两点相遇时,点
两点相遇时,点![]() 停止运动,求点
停止运动,求点![]() 运动的路程一共是多少个单位长度?点
运动的路程一共是多少个单位长度?点![]() 停止的位置所对应的数是多少?
停止的位置所对应的数是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】尺规作图:某学校正在进行校园环境的改造工程设计,准备在校内一块四边形花坛内栽上一棵桂花树.如图,要求桂花树的位置(视为点P),到花坛的两边AB、BC的距离相等,并且点P到点A、D的距离也相等.请用尺规作图作出栽种桂花树的位置点P(不写作法,保留作图痕迹).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com