
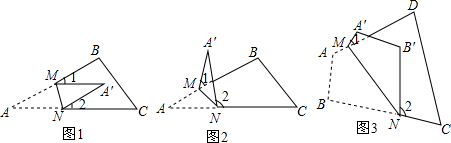
分析 (1)根据三角形的外角的性质即可得到结论;
(2)连接AA′构造等腰三角形,然后结合三角形的外角性质进行探讨证明;
(3)根据平角的定义以及四边形的内角和定理进行探讨.
解答 解:(1)如图1,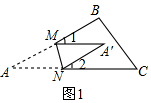
由图形折叠的性质可知,∠CNA′=180°-2∠DNA′…①,∠BMA′=180°-2∠A′MN…②,
①+②得,∠BMA′+∠CNA′=360°-2(∠DNA′+∠A′MN)
即∠BMA′+∠CNA′=360°-2(180°-∠A),
故∠1+∠2=2∠A;
(2)∠2-∠1=2∠A.
证明如下:
如图2,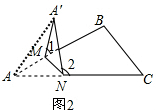
连接AA′构造等腰三角形,
∠BMA′=2∠MA'A,∠CNA'=2∠NA'A,
得∠2-∠1=2∠A,
(3)如图③,
由图形折叠的性质可知∠1=180°-2∠AMN,∠2=180°-2∠BNM,
两式相加得,∠1+∠2=360°-2(∠AMN+∠BNM)
即∠1+∠2=360°-2(360°-∠A-∠B),
所以,∠1+∠2=2(∠A+∠B)-360°.
点评 此题考查三角形的内角和定理,注意此类一题多变的题型,基本思路是相同的,主要运用三角形的内角和定理及其推论进行证明.


 小学教材全测系列答案
小学教材全测系列答案科目:初中数学 来源: 题型:选择题
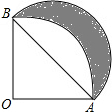 如图,扇形AOB的半径为1,∠AOB=90°,以AB为直径画半圆,则图中的阴影部分的面积为( )
如图,扇形AOB的半径为1,∠AOB=90°,以AB为直径画半圆,则图中的阴影部分的面积为( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$π | C. | $\frac{1}{8}$π | D. | π |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
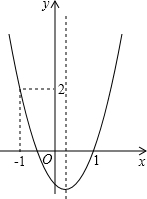 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论中:①abc>0;②2a+b<0;③a+bm<m(am+b);④(a+c)2<b2;⑤a>1.其中正确的是( )
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论中:①abc>0;②2a+b<0;③a+bm<m(am+b);④(a+c)2<b2;⑤a>1.其中正确的是( )| A. | ①⑤ | B. | ①②⑤ | C. | ②⑤ | D. | ①③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 掷一枚硬币,正面向上哥哥赢,反面向上妹妹赢 | |
| B. | 同时掷两枚硬币,两枚都正面向上,哥哥赢,一正一反向上妹妹赢 | |
| C. | 掷一枚骰子,向上的一面是奇数则哥哥赢,反之妹妹赢 | |
| D. | 在不透明的袋子中装有两黑两红四个球,除颜色外,其余均相同,随机摸出一个是黑球则哥哥赢,是红球则妹妹赢 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
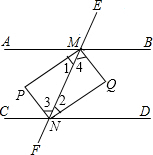 已知:如图,直线AB∥CD,EF和AB、CD分别相交于M、N两点,射线MP、MQ、NP、NQ分别是∠AMN、∠BMN、∠MNC、∠MND的平分线,MP、NP相交于点P,MQ和NQ相交于点Q,求证:四边形MPNQ是矩形.
已知:如图,直线AB∥CD,EF和AB、CD分别相交于M、N两点,射线MP、MQ、NP、NQ分别是∠AMN、∠BMN、∠MNC、∠MND的平分线,MP、NP相交于点P,MQ和NQ相交于点Q,求证:四边形MPNQ是矩形.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com