
【题目】在数学活动课上,老师出示两张等腰三角形纸片,如图所示.图1的三角形边长分别为4,4,2;图2的三角形的腰长也为4,底角等于图1中三角形的顶角;某学习小组将这两张纸片在同一平面内拼成如图3的四边形OABC,连结AC.该学习小组经探究得到以下四个结论,其中错误的是( ) 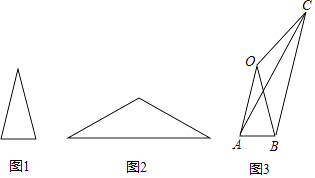
A.∠OCB=2∠ACB
B.∠OAB+∠OAC=90°
C.AC=2 ![]()
D.BC=4 ![]()
【答案】D
【解析】解:A、∵∠OBC=∠AOB, ∴OA∥BC,
∴∠OAC=∠ACB.
∵OA=OC,
∴∠OAC=∠OCA,
∴∠OCA=∠ACB,
∴∠OCB=2∠ACB,结论A正确;
B、∵OA=OB,
∴∠OAB+∠AOB+∠OBA=180°.
∵∠OAC= ![]() ∠OCB=
∠OCB= ![]() ∠AOB,∠OAB=∠OBA,
∠AOB,∠OAB=∠OBA,
∴∠OAB+ ![]() ∠AOB=90°,即∠OAB+∠OAC=90°,结论B正确;
∠AOB=90°,即∠OAB+∠OAC=90°,结论B正确;
C、过点O作OE⊥AB于点E,过点O作OF⊥AC于点F,如图4所示.
∵OA=OB,
∴∠AOE= ![]() ∠AOB=∠OAE.
∠AOB=∠OAE.
在△AOE和△OAE中, 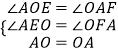 ,
,
∴△AOE≌△OAE(AAS),
∴AF=OE= ![]() =
= ![]() ,
,
∴AC=2AF=2 ![]() ,结论C正确;
,结论C正确;
D、过点B作BM⊥OA于点M,过点O作ON⊥BC于点N,如图5所示.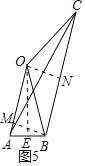
∵∠OAB+∠AOE=90°,∠MAB+∠ABM=90°,
∴∠AOE=∠ABM.
∵∠AEO=∠AMB=90°,
∴△AOE∽△ABM,
∴ ![]() ,
,
∴AM= ![]() ,OM=AO﹣AM=
,OM=AO﹣AM= ![]() .
.
∵BC∥AO,BM⊥AO,ON⊥BC,
∴四边形MBNO为矩形,
∴BN=OM= ![]() .
.
∵OB=OC,ON⊥BC,
∴BC=2BN=7,结论D错误.
故选D.
【考点精析】利用等腰三角形的性质和解直角三角形对题目进行判断即可得到答案,需要熟知等腰三角形的两个底角相等(简称:等边对等角);解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法).


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】一家商店因换季将某种服装打折销售,如果每件服装按标价的5折出售将亏20元,而按标价的8折出售将赚40元.
问:(1)每件服装的标价、成本各是多少元?
(2)为了保证不亏损,最多可以打几折?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一矩形纸片OABC放在平面直角坐标系中,O为原点,点A在x轴上,点C在y轴上,OA=10,OC=8,如图在OC边上取一点D,将△BCD沿BD折叠,使点C恰好落在OA边上,记作E点;
(1)求点E的坐标及折痕DB的长;
(2)在x轴上取两点M、N(点M在点N的左侧),且MN=4.5,求使四边形BDMN的周长最短的点M、点N的坐标。
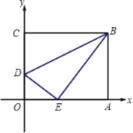
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某校学生对A《最强大脑》、B《朗读者》、C《中国诗词大会》、D《出彩中国人》四个电视节目的喜爱情况,随机抽取了m学生进行调查统计(要求每名学生选出并且只能选出一个自己最喜爱的节目),将调查结果绘制成如下两幅不完整的统计图(如图1和图2):
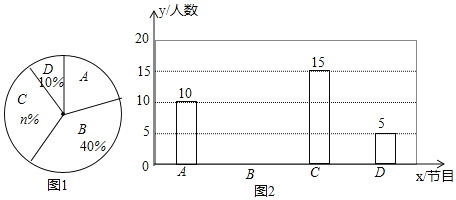
根据统计图提供的信息,回答下列问题;
(1)m= ,n= ;
(2)扇形统计图中,喜爱《最强大脑》节目所对应的扇形的圆心角度数是 度.
(3)根据以上信息直接在答题卡中补全条形统计图;
(4)根据抽样调查结果,请你估计该校6000名学生中有多少学生最喜欢《中国诗词大会》节目.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解方程![]() ﹣1的步骤如下:
﹣1的步骤如下:
(解析)第一步:![]() ﹣1(分数的基本性质)
﹣1(分数的基本性质)
第二步:2x﹣1=3(2x+8)﹣3……(①)
第三步:2x﹣1=6x+24﹣3……(②)
第四步:2x﹣6x=24﹣3+1……(③)
第五步:﹣4x=22(④)
第六步:x=﹣![]() ……(⑤)
……(⑤)
以上解方程第二步到第六步的计算依据有:①去括号法则.②等式性质一.③等式性质二.④合并同类项法则.请选择排序完全正确的一个选项( )
A. ②①③④② B. ②①③④③ C. ③①②④③ D. ③①④②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,半径均为1个单位长度的半圆O1,O2,O3,…组成一条平滑的曲线,点P从原点O出发,沿这条曲线向右运动,速度为每秒![]() 个单位长度,则第2018秒时,点P的坐标是( )
个单位长度,则第2018秒时,点P的坐标是( )
![]()
A. (2016,0) B. (2017,0) C. (2018,0) D. (2017,1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知A(-1,5),B(4,2),C(-1,0)三点.
(1)点A的对称点A′的坐标为(1,-5),点B关于x轴的对称点B′的坐标为________,点C关于y轴的对称点C′的坐标为________;
(2)求(1)中的△A′B′C′的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小林在某商店购买商品A、B若干次(每次A、B两种商品都购买),其中第一、二两次购买时,均按标价购买;第三次购买时,商品A、B同时打折.三次购买商品A、B的数量和费用如表所示.
购买商品A的数量/个 | 购买商品B的数量/个 | 购买总费用/元 | |
第一次购物 | 6 | 5 | 980 |
第二次购物 | 3 | 7 | 940 |
第三次购物 | 9 | 8 | 912 |
(1)求商品A、B的标价;
(2)若商品A、B的折扣相同,问商店是打几折出售这两种商品的?
(3)在(2)的条件下,若小林第四次购物共花去了960元,则小林有哪几种购买方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程解应用题:五莲县新玛特购物中心第一次用5000元购进甲、乙两种商品,其中乙商品的件数比甲商品件数的![]() 倍多15件,甲、乙两种商品的进价和售价如下表(注:获利=售价﹣进价)
倍多15件,甲、乙两种商品的进价和售价如下表(注:获利=售价﹣进价)
甲 | 乙 | |
进价(元/件) | 20 | 30 |
售价(元/件) | 29 | 40 |
(1)新玛特购物中心将第一次购进的甲、乙两种商品全部卖完后一共可获得多少利润?
(2)该购物中心第二次以第一次的进价又购进甲、乙两种商品,其中甲种商品的件数不变,乙种商品的件数是第一次的3倍;甲商品按原价销售,乙商品打折销售,第二次两种商品都销售完以后获得总利润比第一次获得的总利润多160元,求第二次乙种商品是按原价打几折销售?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com