
【题目】在平行四边形ABCD中,连接BD,过点B作BE⊥BD于点B交DA的延长线于点E,过点B作BG⊥CD于点G.
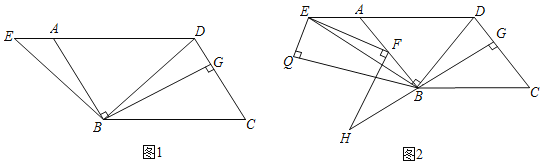
(1)如图1,若∠C=60°,∠BDC=75°,BD=6![]() ,求AE的长度;
,求AE的长度;
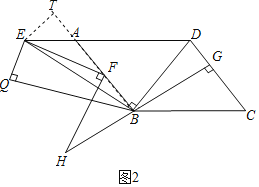
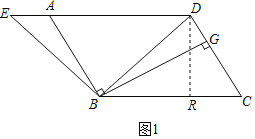
(2)如图2,点F为AB边上一点,连接EF,过点F作FH⊥FE于点F交GB的延长线于点H,在△ABE的异侧,以BE为斜边作Rt△BEQ,其中∠Q=90°,若∠QEB=∠BDC,EF=FH,求证:BF+BH=BQ.
【答案】(1)6﹣2![]() ;(2)详见解析.
;(2)详见解析.
【解析】
(1)根据平行四边形性质可证:△BDE是等腰直角三角形,运用勾股定理可求DE和AD,AE即可求得;
(2)过点E作ET⊥AB交BA的延长线于T,构造直角三角形,由平行四边形性质及直角三角形性质可证:△BEQ≌△BET(AAS),△BFH≌△TEF(AAS),进而可证得结论.
解:(1)如图1,过点D作DR⊥BC于R,
∵ABCD是平行四边形
∴AB∥CD,AD∥BC,AD=BC
∵∠C=60°,∠BDC=75°,
∴∠CBD=180°﹣(∠C+∠BDC)=45°
∴∠ADB=∠CBD=45°
∵BE⊥BD
∴∠DBE=90°
∴∠E=∠BDE=45°
∴DE=![]() BD=12
BD=12
∵DR⊥BC
∴∠BRD=∠CRD=90°
∴∠BDR=∠CBD=45°,
∴DR=BR
由勾股定理可得![]() 即
即![]()
∴DR=BR=6
∵∠C=60°
∴∠CDR=90°﹣60°=30°
∴CR=2![]() ,CD=4
,CD=4![]()
∴AD=BC=DR+CR=6+2![]() ,
,
∴AE=DE﹣AD=12﹣(6+2![]() )=6﹣2
)=6﹣2![]() ;
;
(2)如图2,过点E作ET⊥AB交BA的延长线于T,则∠T=90°
∵ABCD是平行四边形
∴AB∥CD,
∴∠ABD=∠BDC
∵∠QEB=∠BDC
∴∠QEB=∠ABD
∵BG⊥CD,BE⊥BD,FH⊥FE
∴∠BGC=∠ABG=∠DBE=∠EFH=∠Q=90°
∴∠EBT+∠BET=∠EBT+∠ABD=∠EFT+∠BFH=∠EFT+∠FET=90°,
∴∠BET=∠ABD=∠QEB,∠BFH=∠FET
∵BE=BE,EF=FH
∴△BEQ≌△BET(AAS),△BFH≌△TEF(AAS)
∴BQ=BT,BH=FT
∵BF+FT=BT
∴BF+BH=BQ.


 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,点A,B,C都在抛物线y=ax2﹣2amx+am2+2m﹣5(其中﹣![]() <a<0)上,AB∥x轴,∠ABC=135°,且AB=4.
<a<0)上,AB∥x轴,∠ABC=135°,且AB=4.
(1)填空:抛物线的顶点坐标为 (用含m的代数式表示);
(2)求△ABC的面积(用含a的代数式表示);
(3)若△ABC的面积为2,当2m﹣5≤x≤2m﹣2时,y的最大值为2,求m的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC是等边三角形, D、 E分别在边AB、AC上,且AD=CE,CD与BE相交于点O.
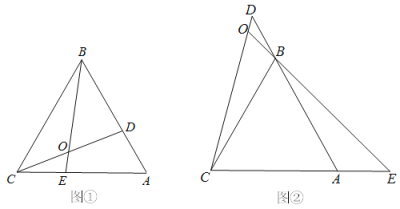
(1)如图①,求∠BOD的度数;
(2)如图②,如果点D、 E分别在边AB、CA的延长线上时,且AD=CE,求∠BOD的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某日,王艳骑自行车到位于家正东方向的演奏厅听音乐会.王艳离家5分钟后自行车出现故障而且发现没有带钱包,王艳立即打电话通知在家看报纸的爸爸骑自行车赶来送钱包(王艳打电话和爸爸准备出门的时间忽略不计),同时王艳以原来一半的速度推着自行车继续走向演奏厅.爸爸接到电话后,立刻出发追赶王艳,追上王艳的同时,王艳坐上出租车并以爸爸速度的2倍赶往演奏厅(王艳打车和爸爸将钱包给王艳的时间忽略不计),同时爸爸立刻掉头以原速赶到位于家正西方3900米的公司上班,最后王艳比爸爸早到达目地的.在整个过程中,王艳和爸爸保持匀速行驶.如图是王艳与爸爸之间的距离y(米)与王艳出发时间x(分钟)之间的函数图象,则王艳到达演奏厅时,爸爸距离公司_____米.
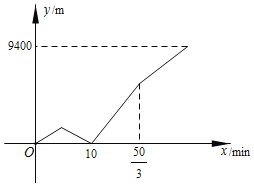
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】毎年6月,学校门口的文具店都会购进毕业季畅销商品进行销售.已知校门口“小光文具店“在5月份就售出每本8元的A种品牌同学录90本,每本10元的B种品牌同学录175本.
(1)某班班长帮班上同学代买A种品牌和B种品牌同学录共27本,共花费246元,请问班长代买A种品牌和B种品牌同学录各多少本?
(2)该文具店在6月份决定将A种品牌同学录每本降价3元后销售,B种品牌同学录每本降价a%(a>0)后销售.于是,6月份该文具店A种品牌同学录的销量比5月份多了![]() a%,B种品牌同学录的销量比5月份多了(a+20)%,且6月份A、B两种品牌的同学录的销售总额达到了2550元,求a的值.
a%,B种品牌同学录的销量比5月份多了(a+20)%,且6月份A、B两种品牌的同学录的销售总额达到了2550元,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某中学举行“中国梦校园好声音”歌手大赛,高、初中部根据初赛成绩,各选出5名选手组成初中代表队和高中代表队参加学校决赛.两个队各选出的5名选手的决赛成绩如图所示.

(1)根据图示填写下表;
平均数(分) | 中位数(分) | 众数(分) | |
初中部 | 85 | ||
高中部 | 85 | 100 |
(2)结合两队成绩的平均数和中位数,分析哪个队的决赛成绩较好;
(3)计算两队决赛成绩的方差并判断哪一个代表队选手成绩较为稳定.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以点P(-1,0)为圆心的圆,交x轴于B、C两点(B在C的左侧),交y轴于A、D两点(A在D的下方),AD=![]() ,将△ABC绕点P旋转180°,得到△MCB.
,将△ABC绕点P旋转180°,得到△MCB.

(1)求B、C两点的坐标;
(2)请在图中画出线段MB、MC,并判断四边形ACMB的形状(不必证明),求出点M的坐标;
(3)动直线l从与BM重合的位置开始绕点B顺时针旋转,到与BC重合时停止,设直线l与CM交点为E,点Q为BE的中点,过点E作EG⊥BC于G,连接MQ、QG.请问在旋转过程中∠MQG的大小是否变化?若不变,求出∠MQG的度数;若变化,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠BAC=90°,AD⊥BC于D,将AB边沿AD折叠,发现B点的对应点E正好在AC的垂直平分线上,则∠C=_______
查看答案和解析>>
科目:初中数学 来源: 题型:
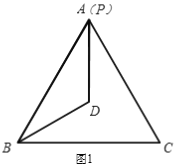
【题目】已知△ABC是等边三角形,P为△ABC所在平面内一个动点,BP=BA,若0°﹤∠PBC﹤ 180°,且∠PBC的平分线上一点D满足DB=DA.
(1)当BP和BA重合时(如图1),则∠BPD=______°.
(2)当BP在∠ABC内部时(如图2),求∠BPD的度数
(3)当BP在∠ABC外部时,请直接写出∠BPD的度数,并画出相应的图形.
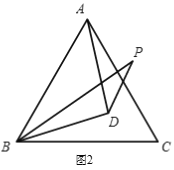
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com