
【题目】如图,在矩形ABCD中,点E是BC边上的一个动点,沿着AE翻折矩形,使点B落在点F处若AB=3,BC=![]() AB,解答下列问题:
AB,解答下列问题:
(1)在点E从点B运动到点C的过程中,求点F运动的路径长;
(2)当点E是BC的中点时,试判断FC与AE的位置关系,并说明你的理由;
(3)当点F在矩形ABCD内部且DF=CD时,求BE的长.
【答案】(1)2π;(2)FC与AE的位置关系为:FC∥AE;(3)![]()
【解析】
(1)根据翻折的性质可得AF=AB,∠BAE=∠EAF,当当点E运动到点C时利用三角函数求出∠BAF的度数,最后再根据弧长公式,求出点F的运动路径长.(2)根据题意知道BE=EF=EC,再利用三角形内角和∠BFE+∠CFE=90°,最后根据翻折的性质求出∠BHE=90°,即可证出FC与AE的位置关系.(3) 过点F作FM⊥AD于点M,延长MF交BC于点N,根据题意求出AM的值,然后利用勾股定理求出MF,根据矩形的性质得到FN, 设BE=x,则EN=![]() ﹣x,利用勾股定理求出BE的长.
﹣x,利用勾股定理求出BE的长.
解:(1)由翻折的性质得:AF=AB,∠BAE=∠EAF,
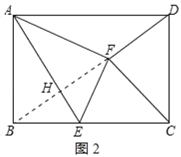
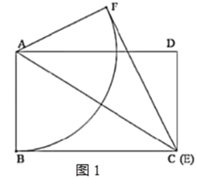
∴点F运动的路径是以A为圆心,AB为半径,∠BAF为圆心角的弧长,如图1所示:
当点E运动到点C时,tan∠BAE=![]() =
=![]()
∴∠BAE=60°,∠BAF=120°,
∴点F的运动路径长为:![]() =2π;
=2π;
(2)FC与AE的位置关系为:FC∥AE;理由如下:
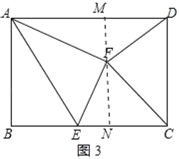
连接BF交AE于点H,如图2所示:
由折叠性质得:BE=EF,
∵BE=CE,
∴BE=EF=EC,
∴∠FBE=∠BFE,∠CFE=∠FCE,
∵∠FBE+∠BFE+∠CFE+∠FCE=180°,
∴∠BFE+∠CFE=90°,即∠BFC=90°,
由折叠的性质得:BF⊥AE,
∴∠BHE=90°,
∴FC∥AE;
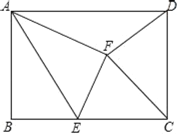
(3)过点F作FM⊥AD于点M,延长MF交BC于点N,如图3所示:
∵AB=3,BC=![]() AB,
AB,
∴BC=3![]() ,
,
∵四边形ABCD是矩形,
∴AB=CD=3,DF=DC=3,
∴AF=DF,
∵MF⊥AD,
∴AM=![]() AD=
AD=![]()
在Rt△MAF中,MF=![]() =
=![]() =
=![]() ,
,
∵∠BAD=∠B=90°,MF⊥AD,
∴四边形ABNM是矩形,
∴BN=AM=![]() ,MN=AB=3,
,MN=AB=3,
∴FN=MN﹣MF=3﹣![]() =
=![]() ,
,
设BE=x,则EN=![]() ﹣x,
﹣x,
由折叠的性质得:FE=BE=x,
在Rt△EFN中,EF2﹣EN2=FN2,
即:x2﹣(![]() ﹣x)2=(
﹣x)2=(![]() )2,
)2,
解得:x=![]() ,
,
∴BE的长为![]() .
.


科目:初中数学 来源: 题型:
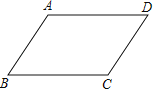
【题目】如图,在平行四边形ABCD中,AD>AB.
(1)作∠BAD的平分线交BC于点E,在AD边上截取AF=AB,连接EF(要求:尺规作图,保留作图痕迹,不写作法);
(2)判断四边形ABEF的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解答下列问题:
(1)阅读理解:
如图1,在![]() 中,若
中,若![]() ,
,![]() ,求
,求![]() 边上的中线
边上的中线![]() 的取值范围.
的取值范围.
解决此问题可以用如下方法:延长![]() 到点
到点![]() 使
使![]() ,再连接
,再连接![]() (或将
(或将![]() 绕着
绕着![]() 逆时针旋转
逆时针旋转![]() 得到
得到![]() ,把
,把![]() 、
、![]() ,
,![]() 集中在
集中在![]() 中,利用三角形三边的关系即可判断.中线
中,利用三角形三边的关系即可判断.中线![]() 的取值范围是______.
的取值范围是______.

(2)问题解决:
如图2,在![]() 中,
中,![]() 是
是![]() 边上的中点,
边上的中点,![]() 于点
于点![]() ,
,![]() 交
交![]() 于点
于点![]() ,
,![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,求证:
,求证:![]() .
.
(3)问题拓展:
如图3,在四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,以
,以![]() 为顶点作一个
为顶点作一个![]() 角,角的两边分别交
角,角的两边分别交![]() ,
,![]() 于
于![]() 、
、![]() 两点,连接
两点,连接![]() ,探索线段
,探索线段![]() ,
,![]() ,
,![]() 之间的数量关系,并加以证明.
之间的数量关系,并加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
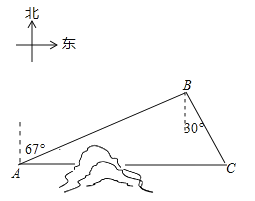
【题目】如图,C地在A地的正东方向,因有大山阻隔,由A地到C地需绕行B地,已知B地位于A地北偏东67°方向,距离A地520km,C地位于B地南偏东30°方向,若打通穿山隧道,建成两地直达高铁,求A地到C地之间高铁线路的长.(结果保留整数)
(参考数据:sin67°≈![]() ,cos67°≈
,cos67°≈![]() ,tan67°≈
,tan67°≈![]() ,
,![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在某市举办的以“校园文明”为主题的中小学生手抄报比赛中,各学校认真组织初赛并按比例筛选出较好的作品参加全市决赛,所有参加市级决赛的作品均获奖,奖项分为一等奖.二等奖、三等奖和优秀奖.现从参加决赛的作品中随机抽取部分作品并将获奖结果绘制成如下两幅统计图请你根据图中所给信息解答下列问题:

(1)一等奖所占的百分比是多少?三等奖的人数是多少?
(2)求三等奖所对应的扇形圆心角的度数;
(3)若参加决赛的作品有3000份,估计获得一等奖和二等奖的总人数有多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
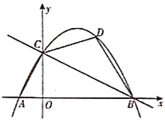
【题目】如图,抛物线![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() .
.
(1)求![]() ,
,![]() 的值;
的值;
(2)若点![]() 是抛物线上的一点,且位于直线
是抛物线上的一点,且位于直线![]() 上方,连接
上方,连接![]() ,
,![]() ,
,![]() .当四边形
.当四边形![]() 的面积有最大值时,求点
的面积有最大值时,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市教育局为了了解线上教学对视力影响,对参加2020年中考的50000名初中毕业生回校后立即进行了一次视力抽样调查,绘制出频数分布表和频数分布直方图的一部分.请根据图表信息回答下列问题:
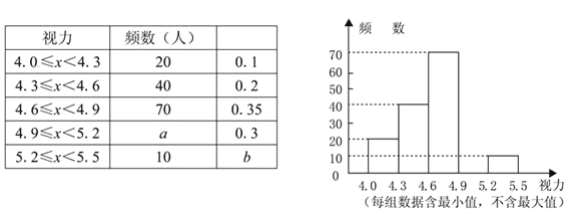
(1)在频数分布表中,a的值为________,b的值为________,并将频数分布直方图补充完整.
(2)甲同学说“我的视力情况是此次抽样调查所得数据的中位数”,问甲同学的视力情况应在什么范围内?
(3)若视力在4.9以上(含4.9)均属正常,求视力正常的人数占被统计人数的百分比,并根据上述信息估计全市初中毕业生中视力正常的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小吴家准备购买一台电视机,小吴将收集到的某地区A、B、C三种品牌电视机销售情况的有关数据统计如下:
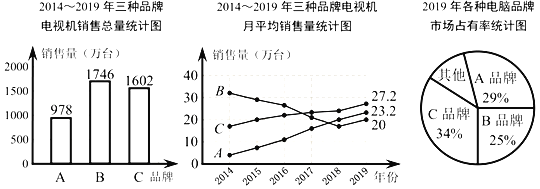
根据上述三个统计图,请解答:
(1)2014~2019年三种品牌电视机销售总量最多的是 品牌,月平均销售量最稳定的是 品牌.
(2)2019年其他品牌的电视机年销售总量是多少万台?
(3)货比三家后,你建议小吴家购买哪种品牌的电视机?说说你的理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com