
 x2上的一个动点.
x2上的一个动点. x2的另一个交点为点Q,连接NP,NQ,求证:∠PNM=∠QNM.
x2的另一个交点为点Q,连接NP,NQ,求证:∠PNM=∠QNM.
 x2),则
x2),则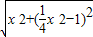 =
= x2+1;
x2+1; x2-(-1)=
x2-(-1)= x2+1
x2+1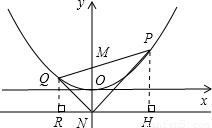
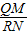 =
=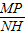 ,
, ,
,

 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案科目:初中数学 来源: 题型:
 里a>0,且a为常数.直线EF和抛物线的对称轴交于点B,和直线x=2交于点D.
里a>0,且a为常数.直线EF和抛物线的对称轴交于点B,和直线x=2交于点D.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,已知点A、B的坐标分别是(0,0)(4,0),将△ABC绕A点按逆时针方向旋转90°后得到△A′B′C′
如图,已知点A、B的坐标分别是(0,0)(4,0),将△ABC绕A点按逆时针方向旋转90°后得到△A′B′C′查看答案和解析>>
科目:初中数学 来源:2011年湖北省宜昌市三中中考数学一模试卷(解析版) 题型:解答题

查看答案和解析>>
科目:初中数学 来源:2012-2013学年广东省广州市荔湾区九年级(上)期末数学试卷(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com