练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    4．把二次函数y=x2-2x+3配方成y=（x-m）2+k的形式，以下结果正确的是（　　）
    A．y=-（x-1）2+4B．y=（x-1）2+2C．y=（x+1）2+2D．y=（x-2）2+3

    分析 根据完全平方公式：加一次项系数一半的平方，即加1，再减1，配成（x-1）2，从而得出结论．

    解答 解：y=x2-2x+3=x2-2x+1-1+3=（x-1）2+2，
    故答案为：B．

    点评 本题考查了二次函数的顶点式，将二次函数配方成顶点式，其实就是一变（变二次项系数为1），二配（配常数项），三合（合成完全平方形式），四合并常数项；其中第2步-配常数项，具体方法是：在二次项系数为1的前提下，加一次项系数一半的平方，得到完全平方式，它有前提“二次项系数为1”，故我们在配顶点式时，如果二次项系数不是1时，总是通过提取二次项系数的办法，使得括号里的式子二次项系数为1，再进行配方即可．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    14．计算：
    （1）（-$\frac{1}{3}$）+（+$\frac{2}{5}$）+（+$\frac{3}{5}$）+（-1$\frac{2}{3}$）
    （2）（-3$\frac{1}{4}$）+（+8$\frac{1}{2}$）-（-5$\frac{3}{4}$）
    （3）（-3$\frac{1}{2}$）-（-$\frac{5}{6}$）+（-0.5）+3$\frac{1}{6}$
    （4）（+3$\frac{2}{5}$）+（-2$\frac{7}{8}$）-（-5$\frac{3}{5}$）-（+$\frac{1}{8}$）
    （5）（-0.25）+（-3）-|-1$\frac{3}{4}$|-（-3）
    （6）（+$\frac{7}{13}$）+（+17）+（-1$\frac{1}{3}$）-（+7）-（-2$\frac{1}{3}$）+（-$\frac{7}{13}$）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    15．在数轴上表示下列各数：-（-4），-|-3.5|，-$\frac{1}{2}$，0，+2.5，1$\frac{1}{2}$，并用“＜”号把这些数连接起来．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    12．已知m＜-1，点（m-1，y1），（m，y2），（m+1，y3）都在函数y=x2的图象上，则（　　）
    A．y1＜y2＜y3B．y1＜y3＜y2C．y3＜y2＜y1D．y2＜y1＜y3

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    19．2016年3月26日，由河北省游泳跳水运动管理中心主办的2016年河北省青少年游泳分站赛在唐山绿洲水上乐园举行，来自保定、秦皇岛灯地区的运动员达440名．在女子4×100米自由泳的比赛中，某教练记录了8组参赛选手的成绩，以240秒为标准，超出的记为正数，不足的记为负数，记录结果如下：
    -13，+2，-8，-15，+3，-9，-5，+5
    （1）在这8组参赛选手中，求成绩最好的一组所用的时间？
    （2）求这8组参赛选手的平均成绩．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

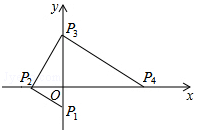    9．如图，点P1，P2，P3，P4均在坐标轴上，且P1P2⊥P2P3，P2P3⊥P3P4，若点P1，P2的坐标分别为（0，-1），（-2，0），求点P4的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    16．如图，一直线与两坐标轴的正半轴分别交于A，B两点，P是线段AB上任意一点（不包括端点），过P分别作两坐标轴的垂线与两坐标轴围成的矩形的周长为10，则该直线的函数表达式是y=5-x．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

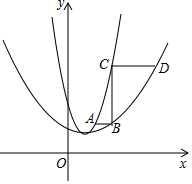    13．若两个二次函数图象的顶点、开口方向都相同，则称这两个二次函数为“同簇二次函数”．
    （1）请写出两个为“同簇二次函数”的函数．
    （2）已知关于x的二次函数y1=2x2-4mx+2m2+1和y2=ax2+bx+$\frac{5}{4}$，其中y1的图象经过点P（1，1），y2与y1为“同簇二次函数”，
    ①求m的值及函数y2的表达式．
    ②如图点A和点C是函数y1上的点，点B和点D是函数y2上的点，且都在对称轴右侧，若AB∥CD∥x轴，BC⊥AB，求$\frac{CD}{AB}$的值（只需直接答案）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    14．已知m-2n=-2，则-3+2m-4n的值为-7．

    查看答案和解析>>

    同步练习册答案