
��ͼ��������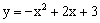 ��x���ཻ��A��B���㣬��y�ύ��C������ΪD�������ߵĶԳ���DF��BC�ཻ�ڵ�E����x���ཻ�ڵ�F��
��x���ཻ��A��B���㣬��y�ύ��C������ΪD�������ߵĶԳ���DF��BC�ཻ�ڵ�E����x���ཻ�ڵ�F��
��1�����߶�DE�ij���
��2�����E��ֱ�����������ཻ��M��x1��y1����N��x2��y2�������жϵ�|x1﹣x2|��ֵ��Сʱ��ֱ��MN��x���λ�ù�ϵ����˵�����ɣ�
��3����PΪx���ϵ�һ�㣬��DAO+��DPO=�Ϧ�����tan�Ϧ�=4ʱ�����P�����꣮

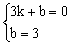 �����
����� .
.

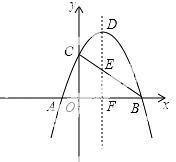
��x1+x2=b1��x1x2=b1﹣3.
��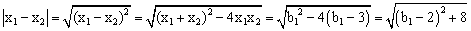 ��
��
�൱b1=2ʱ��|x1﹣x2|��Сֵ=2 .
.
��b1=2ʱ��y=��2﹣b1��x+b1=2����ֱ��MN��x�ᣮ
��3�����ͼ����D��1��4������tan��DOF=4.
�֡�tan�Ϧ�=4�����DOF=�Ϧ�.
�ߡ�DOF=��DAO+��ADO=�Ϧ��� ��DAO+��DPO=�Ϧ������DPO=��ADO.
��DAO+��DPO=�Ϧ������DPO=��ADO.
���ADP�ס�AOD. ��AD2=AO•AP.
��AF=2��DF=4��
��AD2=AF2+DF2=20. ��OP=19.
��P1��19��0����P2�� ﹣17��0����
﹣17��0����
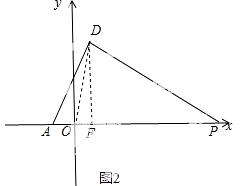


 ȫ��������ϵ�д�
ȫ��������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
��ͼ����ƽ��ֱ������ϵ�У�ֱ��lƽ��x�ᣬ��y���ڵ�A����һ�����ڵĵ�B��l�ϣ�����OB������P�����APQ=90�㣬PQ��x���ڵ�C��
��1��������P���B�غ�ʱ������B�������ǣ�2��1������PA�ij���
��2��������P���߶�OB���ӳ�����ʱ������A�����������B�ĺ�������ȣ���PA��PC��ֵ��
��3��������P��ֱ��OB��ʱ����D��ֱ��OB��ֱ��CA�Ľ��㣬��E��ֱ��CP��y��Ľ��㣬����ACE=��AEC��PD=2OD����PA��PC��ֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
��ͼ����A��B��C��D�ڡ�O�ϣ�O���ڡ�D���ڲ����ı���OABCΪƽ���ı��Σ����OAD+��OCD= �㣮
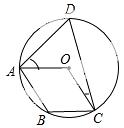
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
������x�������y��������Щ�����ɫ��������������Ӻ������ȡһ�������Ǻ���ĸ�����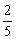 �����������ٷ�
�����������ٷ� ��1��������ʱȡ�ú���ĸ��ʱ�Ϊ
��1��������ʱȡ�ú���ĸ��ʱ�Ϊ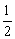 ��
��
��1����գ�x= ��y= ��
��2��С����С������x�������y���������������Ϸ��Լ�����Ӻ��������ȡһ�������Ŵ�ʣ�µ������������ȡһ������������ɫ��ͬ��С��ʤ������ɫ��ͬ��С��ʤ���������˻�ʤ�ĸ��ʸ��Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����ʽ����ȷ���ǣ�������
| �� | A�� | ��a��b��2=a2��2ab+b2 | B�� | ��a��b��2=a2��b2 | C�� | ��a��b��2=a2+2ab+b2 | D�� | ��a��b��2=a2��ab+b2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
��֪��A������Ϊ��2��0������P��ֱ��y=x���˶������Ե�PΪԲ�ģ�PA�ij�Ϊ�뾶��Բ�������Сʱ����P������Ϊ��������
| �� | A�� | ��1����1�� | B�� | ��0��0�� | C�� | ��1��1�� | D�� | �� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
���е����У��ʺ����ղ鷽ʽ���ǣ� ��
A�������ɽ��������������
B�������ɽ�е���̨ij��Ŀ��������
C�������ɽ�����ͥ�ճ�����֧�����
D�������ɽ��ijУij��ѧ���ԡ�������ɽ����֪����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
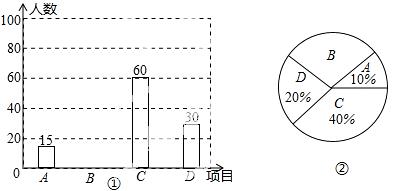
Ϊ�ƹ�������������μ䡱�������ij��ѧ������ѧ���п���A��ʵ����B��������Զ��C��������D���ܲ����ֻ��Ŀ��Ϊ���˽�ѧ����������Ŀ��ϲ������������ȡ�˲���ѧ�����е��飬�������������Ƴ���ͼ�٢ڵ�ͳ��ͼ������ͼ�е���Ϣ����������⣺
��1������������У��������˶�����ѧ����
��2������㱾�������ϲ����������Զ����ѧ����������ռ�ٷֱȣ���������ͳ��ͼ����������
��3�������鵽ϲ������������5��ѧ������3��������2��Ů�����ִ���5��ѧ���������ȡ2��ѧ�������û���״ͼ���б��ķ��������
 �պó鵽ͬ�Ա�ѧ���ĸ��ʣ�
�պó鵽ͬ�Ա�ѧ���ĸ��ʣ�
 ��
��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com