
【题目】阅读下列材料:
数学课上,老师出示了这样一个问题:
如图1,正方形为![]() 中,点
中,点![]() 、
、![]() 在对角线
在对角线![]() 上,且
上,且![]() ,探究线段
,探究线段![]() 、
、![]() 、
、![]() 之间的数量关系,并证明.
之间的数量关系,并证明.
某学习小组的同学经过思考,交流了自己的想法:
小明:“通过观察和度量,发现![]() 与
与![]() 存在某种数量关系”;
存在某种数量关系”;
小强:“通过观察和度量,发现图1中线段![]() 与
与![]() 相等”;
相等”;
小伟:“通过构造![]() (如图2),证明三角形全等,进而可以得到线段
(如图2),证明三角形全等,进而可以得到线段![]() 、
、![]() 、
、![]() 之间的数量关系”.
之间的数量关系”.
老师:“此题可以修改为‘正方形![]() 中,点
中,点![]() 在对角线
在对角线![]() 上,延长
上,延长![]() 交
交![]() 于点
于点![]() ,在
,在![]() 上取一点
上取一点![]() ,连接
,连接![]() (如图3).如果给出
(如图3).如果给出![]() 、
、![]() 的数量关系与
的数量关系与![]() 、
、![]() 的数量关系,那么可以求出
的数量关系,那么可以求出![]() 的值”.
的值”.

请回答:
(1)求证:![]() ;
;
(2)探究线段![]() 、
、![]() 、
、![]() 之间的数量关系,并证明;
之间的数量关系,并证明;
(3)若![]() ,
,![]() ,求
,求![]() 的值(用含
的值(用含![]() 的代数式表示).
的代数式表示).
 科学实验活动册系列答案
科学实验活动册系列答案科目:初中数学 来源: 题型:
【题目】为了预防流感,某学校在休息日用药熏消毒法对教室进行消毒. 已知药物释放过程中,室内每立方米空气中的含药量y(mg)与时间t(h)成正比;药物释放完毕后,y与t之间的函数解析式为y=![]() (a为常数),如图所示. 根据图中提供的信息,解答下列问题:
(a为常数),如图所示. 根据图中提供的信息,解答下列问题:
(1)写出从释放药物开始,y与t之间的两个函数解析式及相应的自变量取值范围;
(2)据测定,当空气中每立方米的含药量降低到0.25mg以下时,学生方可进入教室,那么药物释放开始,至少需要经过多少小时,学生才能进入教室?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在纸面上有一条数轴
![]()
操作一:
折叠数轴,使表示1的点与表示-1的点重合,则表示-5的点与表示 的点重合.
操作二:
折叠数轴,使表示1的点与表示3的点重合,在这个操作下回答下列问题:①表示-2的点与表示 的点重合;
②若数轴上A,B两点的距离为7(A在B的左侧),且折叠后A,B两点重合,则点A表示的数为 ,
点B表示的数为
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解八年级男生立定跳远测试情况,随机抽取了部分八年级男生的测试成绩进行统计,根据评分标准,将他们的成绩分为优秀、良好、及格、不及格四个等级,以下是根据调查结果绘制的统计图表的一部分.
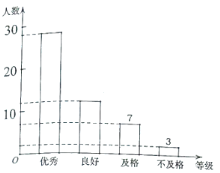
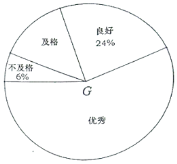
根据以上信息,解答下列问题:
(1)被调查的男生中,成绩等级为不及格的男生人数有__________人,成绩等级为良好的男生人数占被调查男生人数的百分比为__________%;
(2)被调查男生的总数为__________人,条形统计图中优秀的男生人数为__________人;
(3)若该校八年级共有300名男生,根据调查结果,估计该校八年级男生立定跳远测试成绩为良好和优秀的男生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个装有进水管和出水管的容器,从某时刻开始的4分钟内只进水不出水,在随后的8分钟内既进水又出水,接着关闭进水管直到容器内的水放完.假设每分钟的进水量和出水量保持不变,容器内水量![]() (单位:
(单位:![]() )与时间
)与时间![]() (单位:
(单位:![]() )的部分函数图象如图所示,请结合图象信息解答下列问题:
)的部分函数图象如图所示,请结合图象信息解答下列问题:
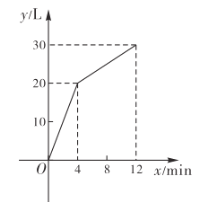
(1)求出水管的出水速度;
(2)求![]() 时容器内的水量;
时容器内的水量;
(3)从关闭进水管起多少分钟时,该容器内的水恰好放完?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠A=90°,AB=AC=![]() +2,D是边AC上的动点,BD的垂直平分线交BC于点E,连接DE,若△CDE为直角三角形,则BE的长为_____.
+2,D是边AC上的动点,BD的垂直平分线交BC于点E,连接DE,若△CDE为直角三角形,则BE的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2018年1月25日,济南至成都方向的高铁线路正式开通,高铁平均时速为普快平均时速的4倍,从济南到成都的高铁运行时间比普快列车减少了26小时.已知济南到成都的火车行车里程约为2288千米,求高铁列车的平均时速.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com