
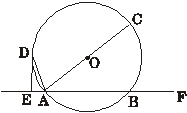
如图,直线EF交⊙O于A、B两点,AC是⊙O直径,AD平分∠CAE交⊙O于点D,且DE⊥EF,垂足为E.
(1)求证:DE是⊙O的切线;
(2)若DE=4cm,AE=2cm,求⊙O的半径.
 |
科目:初中数学 来源: 题型:
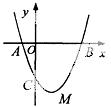
如图,在直角坐标系xOy中,抛物线y=x2+bx-3与x轴交于A、B两点,与y轴交于点C,顶点为M,已知A(-1,0).
(1)则顶点M的坐标为 ;
(2)当y>0时,试写出x的范围,并求A、B两点间的距离;
(3)在抛物线曲线段BMC上有一动点D,求四边形OBDC面积的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,河流的两岸PQ,MN互相平行,河岸PQ上有一排小树,已知相邻两树之间的距离CD=50米,某人在河岸MN的A处测的∠DAN=35°,然后沿河岸走了120米到达B处,测的∠CBN=70°,
求河流的宽度CE(结果保留两个有效数字).
(参考数据:
sin35°≈0.57,cos35°≈0.82,tan35°≈0.70
Sin70°≈0.94,cos70°≈0.34,tan70°≈2.75)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com